
移動系では、静止時に比べ電磁波の往復距離が伸びる。 生じる電磁力の強さは距離の2乗に反比例する為、移動系では電磁力が弱まると思える。 しかし、マックスウェルの方程式では、全ての系で生じる電磁力の強さは同じである。 この矛盾の解法には、光速度不変の原理と物質の収縮の2通りがある。
マックスウェルの方程式では、真空の誘電率と真空の透磁率を定数としている。この2つは電磁波の伝播速度を決定する要素であり、
定数としていることから、静止系と移動系とを区別せず、全ての系において電磁力(=光)は、
空間を一定速度(c[m/s])で伝わるとしている。現実にも、移動系においても、生じる電磁力の強さは静止系と変わらない。
ここから、「光速度不変の原理」が導かれている。
プラス又はマイナスの電荷を持つ物質同士は電磁波(=光)を交換し合い、両者間には作用反作用の形で、
引力又は斥力が働く。電磁波は両物質間を光速で行き来し、生ずる引力又は斥力の強さは、物質間の距離の二乗に反比例し、
電荷の強さに比例する。
移動系では、電磁波の往復距離が伸びる為、電磁力は弱まると思える。
しかし、実際には電磁力の強さは不変である。電磁力の往復に要する時間は、全ての系において等しい。
従って、物質の移動に関わらず、物質とその間を往復する電磁波(光)との相対速度は不変であると考える必要がある様にも思われる。
目次へ
 電荷を帯びた粒子OとPを設定し、OP間の距離をc[m]と仮定する。PはOを中心とする円
電荷を帯びた粒子OとPを設定し、OP間の距離をc[m]と仮定する。PはOを中心とする円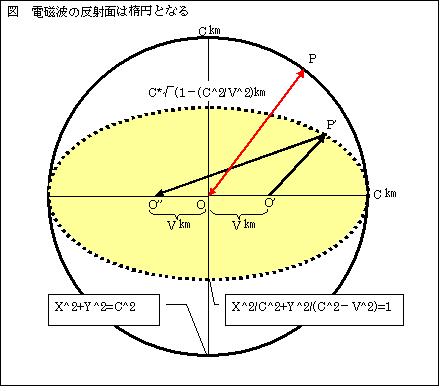 しかし、実際の光の相対速度は、√(c2+v2-2cv*cosθ)[m/s]である。なのに何故、
マックスウェルの方程式通りの引力又は斥力が生じるのか。
しかし、実際の光の相対速度は、√(c2+v2-2cv*cosθ)[m/s]である。なのに何故、
マックスウェルの方程式通りの引力又は斥力が生じるのか。