
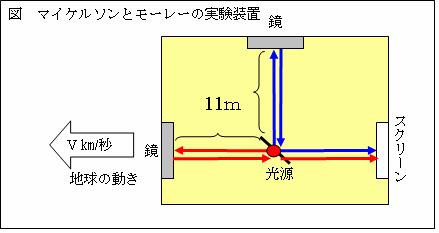
マイケルソンとモーレーは、観測者Aが移動しながら光の速度を測ると、光の進む方向によりその相対速度は異なると考えました。そこで、下図の様な「マイケルソン干渉計」を考案しました。
地球は左方向へv[m/s]で移動しています。装置も地球と一緒に移動しています。そして、鏡により光を地球の進行方向(横方向=赤の矢印)と上下左右方向(縦方向=青の矢印)に片道11[m]の距離を往復させました。
説明の便宜上、光の片道をc[m]とします。静止時の往復時間=2秒です。光の絶対速度はc[m/s]なので、光の往復距離は、2c[m]です。また
v慣性系の横方向の往復時間=c/(c-v)+c/(c+v)=2c2/(c2-v2)=2/(1-v2/c2)秒
です。光の絶対速度はc[m/s]なので
v慣性系の光の横往復距離= c[m/s]×2/(1-v2/c2)秒=2c/(1-v2/c2)[m]
です。従って、v慣性系での光の横往復距離は、静止時の2c/(1-v2/c2)[m]÷2c[m]=1/(1-v2/c2)倍となっていることが分かります。
一方
v慣性系の縦方向の往復時間=2c/√(c2-v2)=2/√(1-v2/c2)秒です。光の絶対速度はc[m/s]なので
v慣性系の光の縦往復距離= c[m/s]×2/√(1-v2/c2)秒=2c/√(1-v2/c2)[m]
です。従って、v慣性系での光の縦往復距離は、静止時の2c/√(1-v2/c2)[m]÷2c[m]=1/√(1-v2/c2)倍となっていることが分かります。
そうすると、マイケルソンとモーレーの実験装置では、横方向に往復した光と縦方向に往復した光とは、移動距離が異なる為に、同時には戻って来ることは出来ない筈です。
しかし、実験の結果、赤と青の2本の光は同時に戻って来たのです。
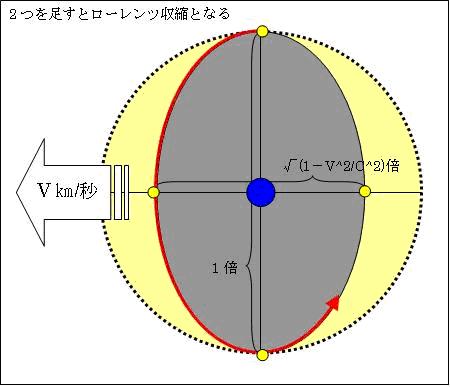
この実験結果を説明する為に、ローレンツは、装置自体が横方向に√(1-v2/c2)倍収縮したと考えました。これを「ローレンツ収縮」と言います。これで
横方向の光の往復距離=2c√(1-v2/c2)/(1-v2/c2)[m]=2c/√(1-v2/c2)[m]=縦方向の光の往復距離
となり、2本の光は同時に戻ることが出来たのです。
 以上の内容を、アインシュタイン博士自身が書かれた『特殊及び一般相対性理論について』では次のように記述されています。
以上の内容を、アインシュタイン博士自身が書かれた『特殊及び一般相対性理論について』では次のように記述されています。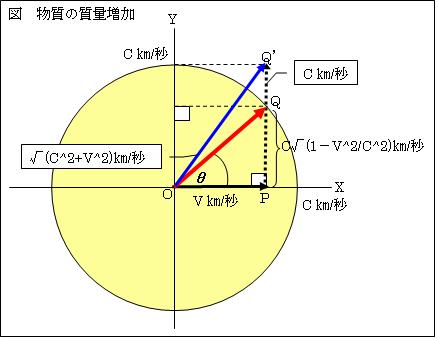 次に、物質が進行方向に√(1-v2/c2)倍「ローレンツ収縮」する仕組みを説明します。
次に、物質が進行方向に√(1-v2/c2)倍「ローレンツ収縮」する仕組みを説明します。
