僽儔僢僪儕乕偺岝峴嵎幃偱朷墦嬀偼廲併(1-v2/c2)廂弅偟偰偄傞
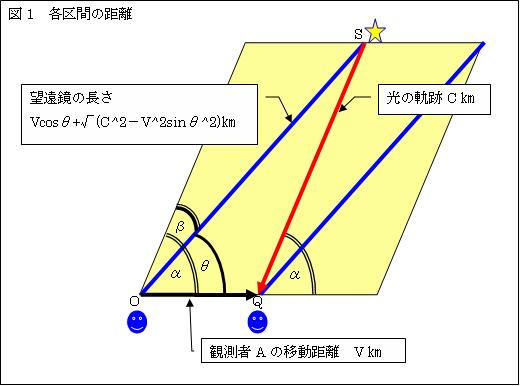
丂嘥.惎傪朷墦嬀偱尒傞応崌丄幚嵺偵惎偺偁傞曽岦偵朷墦嬀傪岦偗偰傕丄偦偺惎偼尒偊側偄偙偲偑抦傜傟偰偄傞丅
彮偟抧媴偺恑峴曽岦偵朷墦嬀傪孹偗偰傗傜側偄偲丄偦偺惎偼尒偊側偄丅
丂嘦.惵慄OS傪朷墦嬀偲偡傞丅朷墦嬀偲娤應幰偼丄懍搙v[m/s]偱O偐傜Q傊堏摦偡傞丅惎S偐傜偺岝傪愒偺栴報SQ偲偡傞丅
朷墦嬀傪佢兛孹偗偨偺偱偼丄惎S偐傜偺岝偼朷墦嬀傪捠傝敳偗傞偙偲偼弌棃側偄丅
佢兤孹偗偰傗傞偲丄岝偼忋庤偵朷墦嬀傪捠傝敳偗偰Q偺埵抲偺娤應幰偵撏偔丅偙偺佢兛偲佢兤偺嵎偱偁傞佢兝偑岝峴嵎偱偁傞丅
丂嘨.偙偺岝峴嵎偼丄僽儔僢僪儕乕偺幃
sin兝=(v/c)sin兛
偲偟偰昞傢偝傟傞丅
丂嘩.曋媂忋丄SQ=c[m]丄OQ=v[m]偲偡傞丅岝偼1昩偱惎S偐傜Q偺埵抲偺娤應幰偵撏偔丅娤應幰偼1昩偱O偐傜Q傊堏摦偡傞丅偙偺帪丄
朷墦嬀OS偺挿偝傪a偲偡傞偲
a=vcos兤+併(c2-v2sin兤2)[m]
偲側傞丅a偺摫弌曽朄偼埲壓偺捠傝偱偁傞丅戞擇梋尫掕棟傛傝
SQ=併(a2+v2-2avcos兤)=c
偱偁傞丅廬偭偰
a2-2vcos兤*a+ v2-c2=0
偙偺擇師曽掱幃偺惓偺夝偼
a= vcos兤+併(v2cos兤2-v2+ c2)
= vcos兤+併(c2-v2sin兤2)[m]
偲側傞丅
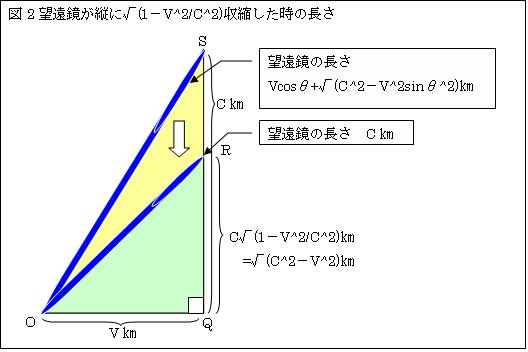
丂嘪.暔幙偑崅懍偱堏摦偡傞偲丄廲偵併(1-v2/c2)丄
墶偵(1-v2/c2)廂弅偡傞丅
偙偺條偵廂弅偟偮偮懍搙v[m/s]偱堏摦偡傞偲丄岝偵偲偭偰暔幙偼廲偵
併(1-v2/c2)廂弅偟偨宍偲側傞丅
丂(徻嵶偼僩僢僾儁乕僕俁侾丏暔幙偺廂弅偵傛傞戞嶰曄姺傪嶲徠壓偝偄)
丂嘫.曋媂忋丄仮OQS傪捈妏嶰妏宍偲偡傞丅SQ偼併(1-v2/c2)廂弅偡傞偺偱丄
SQ仺RQ=c併(1-v2/c2)=併(c2-v2)[m]
偲側傞丅廬偭偰丄朷墦嬀偺挿偝偼
OS仺OR=併(OQ2+RQ2)=併(v2+c2-v2)=c[m]
偲側傞丅偙偺帪丄恾1偺SQ偼OS=a=c側偺偱
SQ=併(a2+v2-2avcos兤)=併(c2+v2-2cvcos兤)[m]
偲側傞丅
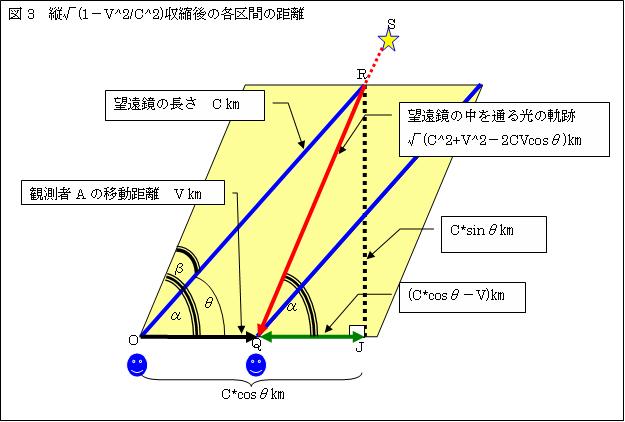 丂嘮.廬偭偰丄廂弅屻偺奺嬫娫偺嫍棧偼丄恾3偺捠傝偲側傞丅朷墦嬀偺抂R偐傜OQ偺墑挿慄忋偵壓傠偟偨悅慄偺懌傪J偲偡傞丅
RJ= c*sin兤[m]丄OJ= c*cos兤[m]丄QJ=(c*cos兤-v)[m]偱偁傞丅
丂嘮.廬偭偰丄廂弅屻偺奺嬫娫偺嫍棧偼丄恾3偺捠傝偲側傞丅朷墦嬀偺抂R偐傜OQ偺墑挿慄忋偵壓傠偟偨悅慄偺懌傪J偲偡傞丅
RJ= c*sin兤[m]丄OJ= c*cos兤[m]丄QJ=(c*cos兤-v)[m]偱偁傞丅
丂偙偺嫍棧愝掕偱丄僽儔僢僪儕乕偺幃傪媮傔傞丅
sin兛= c*sin兤/併(c2+v2
-2vccos兤)
sin兝= sin(兛-兤)= sin兛*cos兤-cos兛*sin兤丂(岞幃傛傝)
= (c*sin兤/併(c2+v2-2vccos兤))* cos兤-((c*cos兤-v)/ 併(c2+v2-2vccos兤))
* sin兤
= (sin兤/併(c2+v2-2vccos兤))*(c* cos兤-c*cos兤+v)= v* sin兤/
併(c2+v2-2vccos兤)
亪sin兝=(v/c)sin兛
偲丄僽儔僢僪儕乕偺幃偑摫偐傟傞丅
丂偙偺條偵丄朷墦嬀偑廲偵併(1-v2/c2)廂弅偟偨帪偵丄僽儔僢僪儕乕偺幃偼惉棫偡傞丅


 丂嘮.廬偭偰丄廂弅屻偺奺嬫娫偺嫍棧偼丄恾3偺捠傝偲側傞丅朷墦嬀偺抂R偐傜OQ偺墑挿慄忋偵壓傠偟偨悅慄偺懌傪J偲偡傞丅
RJ= c*sin兤[m]丄OJ= c*cos兤[m]丄QJ=(c*cos兤-v)[m]偱偁傞丅
丂嘮.廬偭偰丄廂弅屻偺奺嬫娫偺嫍棧偼丄恾3偺捠傝偲側傞丅朷墦嬀偺抂R偐傜OQ偺墑挿慄忋偵壓傠偟偨悅慄偺懌傪J偲偡傞丅
RJ= c*sin兤[m]丄OJ= c*cos兤[m]丄QJ=(c*cos兤-v)[m]偱偁傞丅