ニュートンは、重力は瞬時に伝わる力であるとしました。これに対して、特殊相対性理論では、
重力は電磁力と同じく光速で伝わる力であると設定しました。強い力と弱い力及び光も光速で伝わります。
物質も光速以上の速度で移動することは出来ません。
つまり、この宇宙には瞬時に伝わる影響力や因果関係は存在しないとされています。
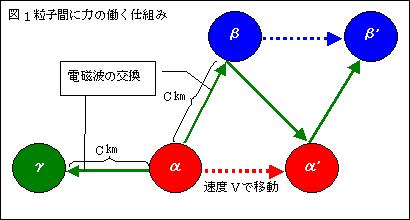
物質αとβ及びγがあり、その距離をc[m]とし、βとγの電荷は等しいと仮定します。αとβには、
電磁波を交換し合うことで、引力又は斥力の電磁力が働きます。電磁波が瞬時に伝わるのであれば、
αはβの時空間上の位置を特定出来ます。
電磁力の強さは距離の2乗に反比例します。従って、αに働いた電磁力の強さと方向より、その瞬間βはこの位置に在ると特定出来ます。
αとβ・αとγ双方で生じた電磁力の強さが同じであれば、αβとαγの距離は等しく、同時にαが発した電磁波は、
同時にβとγに届いたことが分かります。
この様に、瞬時に伝わる力があれば、ある事象が起こった時と場所を特定することが出来ます。
そして、2つの事象が同時に起こったのか否かを正しく知ることが出来ます。この時、同時性は絶対的です。
電磁力が空間を光速で伝わると、何が変わって来るのでしょうか。
速度vで移動しながら、αβγが電磁波を交換し合います。αβγと電磁波との相対速度は
√(c2+v2-2cvcosθ)[m/s]です(第二余弦定理より)。
縦方向はcosθ=v/cなので
縦方向の電磁波の往復時間=2c/√(c2-v2)=2/√(1-v2/c2)秒
です。よって
縦方向の電磁波の往復距離=2c/√(1-v2/c2)[m]
です。横方向の往路はcosθ=1、復路はcosθ=-1なので
横方向の電磁波の往復時間=c/(c-v)+c/(c+v)= 2/(1-v2/c2)秒
です。よって
横方向の電磁波の往復距離=2c/(1-v2/c2)[m]
です。
電磁力の強さは距離の2乗に反比例するので、移動系では、速度vと方向θにより生じる電磁力の強さが異なる様に思えます。
しかし、マックスウェルの電磁力の方程式では、静止系と移動系とを区別せず、生じる電磁力の強さは同一としています。
そして、現実にそうなります。
この矛盾を解消する為、電磁波の相対速度は、αβγが移動しても変化せず常にc[m/s]であるとする「光速度不変の原理」
が導かれました。これにより、速度vで移動する慣性系でも、電磁波が往復するのに要する時間は、
縦方向横方向共に2c/c=2秒となります。これでαβ間・αγ間に働く電磁力の強さは、
移動速度や方向に関係なく静止時と同値となれます。
もう１つは、速度vで移動する慣性系では、物質は縦方向に√(1-v2/c2)、
横方向に(1-v2/c2)収縮すると設定します。これにより
縦方向の電磁波の往復距離=2c√(1-v2/c2)/√(1-v2/c2)=2c[m]
横方向の電磁波の往復距離=2c(1-v2/c2)/(1-v2/c2)[m]=2c[m]
となり、電磁波の往復距離は、速度vや角度θに関係なく静止時と等しく、生じる電磁力の強さも静止時と同値となります。
物質を構成する粒子と粒子とは、接し合っている訳ではありません。両者間に働く引力と斥力とが釣り合う距離を保っています。
その距離をcと仮定します。物質が速度vで移動すると、粒子間の相対距離が縦方向に√(1-v2/c2)、
横方向に(1-v2/c2)収縮すれば、引力及び斥力の往復距離は2cとなり、両者が釣り合う距離となります。
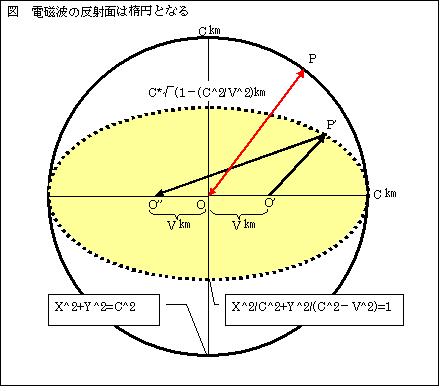
αからc[m]の距離は
X2+Y2=c2
の円で表されます。静止時には、この円周上にβやγがあり、O位置にあるαから発せられた電磁波は円周上Pでβやγにより反射され、
再びαに戻って来ます。その往復距離は2cです。
速度vで移動すると、粒子間の距離は縦方向に√(1-v2/c2)、横方向に(1-v2/c2)
収縮します。O'位置のαから発せられた電磁波がP'位置のβやγにより反射された点を結ぶと
X2/c2+Y2/(c2-v2)=1
の楕円となります。楕円の2つの焦点と任意の楕円上の点を結ぶ長さO'P'O''は常に2cであり、電磁波の往復距離は静止時と同じです。
この様に、電磁波の相対速度と粒子間の距離は変わらないと仮定して、マックスウェルの方程式を移動する慣性系でそのまま使用しても、
電磁波の相対速度と粒子間の距離の収縮とを考慮して計算しても、算出される電磁力の強さは同じとなります。
これは、光速で伝わる重力・強い力・弱い力全てに言えることです。
前者の考え方によれば、移動する慣性系でも、βやγの位置はX2+Y2=c2の円周上にあり、
同時にαから発せられた電磁力をβやγは同時に反射したことになります。後者の考え方によれば、
同時にαから発した電磁波を反射した時の、
βやγの位置はX2/c2+Y2/(c2-v2)=1の楕円上にあり、
反射した時はそれぞれ異なることとなります。往復の合計距離は等しいのですが、往路と復路の距離は楕円上の位置により異なるからです。
この様に、瞬時に伝わるものが無いと、ある事象の起こった時と場所とを特定することは出来なくなります。
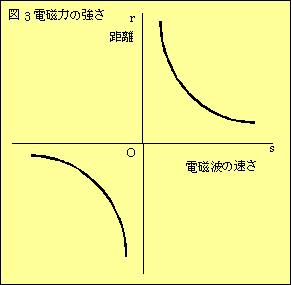
αにはβから来る電磁波の方向と強さしか分かりません。電磁波の量は距離の2乗に反比例するので、
電磁波の速度が速くなれば交換される電磁波は多くなり、距離が遠くなれば電磁波は少なくなります。
F=k*s*r (k=定数、s=電磁波の速度、r=物質間の距離)
の関係が成り立ちます。従って、βまでの距離を特定することは出来ず、βが電磁波を反射した時も特定することは出来ません。
しかし、αには、電磁波を反射した時のβの時空間上の位置は意味がありません。βからやってくる電磁波の方向と量に応じた
電磁力が、αには働くだけだからです。
哲学上、事象の起こった時と場所を特定することは重要かも知れません。しかし、
光速度は不変で粒子間の距離は変化しないと仮定して計算した通りに物質は動きます。物理学上
電磁波は、上記の円周上で同時に反射されたのか否かは分からないけれども、同時と考えて良いのです。この様な意味で、
同時性は相対的なものとなります。
