仛戞堦晹岝懍搙丂
嬤擔揰偺堏摦
儅僢僋僗僁僄儖
儅僀働儖僜儞偲儌乕儗乕
岝峴嵎
c-vcos兤
暔幙廂弅
帺慠揘妛
暔幙曄壔
惷巭宯
岝懍搙晄曄偺梫惪
媡曄姺
儗乕僓乕
懍搙偺壛朄懃
墶僪僢僾儔乕
帪嬻娫偺曄壔
儘乕儗儞僣廂弅
儕儞僌儗乕僓乕僕儍僀儘
摨帪惈偺憡懳惈
僂儔僔儅岠壥
暔幙攇
媡曄姺壜擻側昁梫廫暘忦審亄儘乕儗儞僣場巕=儘乕儗儞僣曄姺
1.儘乕儗儞僣曄姺偺暘曣偼壗屘丄併乮1-v2/c2乯側偺偐
丂儘乕儗儞僣曄姺偲偼丄師偺曄姺幃傪尵偄傑偡丅
t'= (t-vx/c2) / 併乮1-v2/c2乯
倶'=(x-v倲)/併乮1-v2/c2乯
y'= y丂
z'= z丂
丂帪娫倲丄媦傃恑峴曽岦偱偁傞師尦倶偺曄姺幃偺暘曣偑併(1-v2/c2)偲側傞偺偼壗屘偱偟傚偆偐丅
2.惷巭宯
丂傾僀儞僔儏僞僀儞攷巑偺僀儊乕僕偡傞塅拡偼丄嬻側嬻娫傪岝傗暔幙偺棻巕偑堏摦偡傞傕偺偱偡丅偦偺僀儊乕僕偱偼丄
惷巭偟偰偄傞宯傪帵偡偙偲偼弌棃傑偣傫丅恀嬻偼杮摉偵壗傕柍偄嬻娫偲側傝丄偦偺埵抲傪峫偊傞偙偲偼弌棃傑偣傫丅
廬偭偰丄塅拡偵偼暔幙偟偐側偔丄塣摦偲偼懠偺暔幙偲偺憡懳揑埵抲娭學偲側傝傑偡丅
丂偦偆側傞偲丄堦曽偑惷巭偟偰偍傝懠曽偑堏摦偟偰偄傞偲尒偊偰傕丄媡偵懠曽偑惷巭偟偰偍傝堦曽偑堏摦偟偰偄傞偲傕峫偊傜傟傑偡丅
偮傑傝丄曕偄偰偄傞巹偑慜偵恑傫偱偄傞偺偐丄巹埲奜偺慡塅拡偑屻傠偵堏摦偟偰偄傞偺偐帵偡偙偲偑弌棃側偔側傝傑偡丅
堏摦傪敾抐偡傞婎弨乮愨懳惷巭偺堦揰乯偑側偄偺偱丄惷巭宯偲尵偆摿尃傪帩偮傕偺偼柍偔丄
乽慡偰偺姷惈宯偼摨摍乿偲側傝傑偡丅
3.曄姺媦傃媡曄姺
丂偁傞姷惈宯傪惷巭偲尒傞偲丄懠偺姷惈宯偼堏摦偟偰偄傞丅偦偺媡偺尒曽傕弌棃傑偡丅廬偭偰丄摨堦偺曄姺幃偱慡偰偺姷惈宯偐傜
慡偰偺姷惈宯偵丄曄姺枖偼媡曄姺弌棃側偗傟偽側傝傑偣傫丅
丂惷巭偟偰偄傞偲尒傞姷惈宯A偺岝(x,y,z,t)傪丄堏摦偡傞偲尒傞姷惈宯B偐傜尒偨岝(x',y',z',t')偵曄姺偟傑偡丅
惷巭宯偑柍偗傟偽丄崱搙偼惷巭偟偰偄傞偲尒傞B姷惈宯偺岝(x',y',z',t')傪丄v傪-v偵偟偨摨偠曄姺幃偵傛傝丄
(x,y,z,t)傪(x',y',z',t')偵偟偰媡曄姺偡傞偲丄堏摦偟偰偄傞偲尒傞姷惈宯A偺尦偺岝(x,y,z,t)偵栠傜側偗傟偽側傝傑偣傫丅
儅僢僋僗僂僃儖偺曽掱幃偑丄偁傜備傞姷惈宯偱巊偊傞堊偵偼丄曄姺屻偺揹帴攇(=岝)偼丄忢偵c偲側傞曄姺幃偱側偔偰偼側傝傑偣傫丅
4.曄姺丒媡曄姺偟偨屻偺岝偑丄忢偵c偲側傜側偗傟偽側傜側偄棟桼
丂偟偐偟丄嬻娫偵壗傜偐偺幚懱偑偁傟偽丄偦偺埵抲傪峫偊傞偙偲偑弌棃傑偡丅偦偆偡傞偲丄偦偺嬻娫偑惷巭宯偱偁傝丄
暔幙偼偦偺惷巭宯傪婎弨偵偟偰丄堏摦偟偰偄傞偐斲偐敾抐弌棃傑偡丅嬻娫偵偼丄岝傪堦掕懍搙偱揱偊偰偄傞傕偺偑懚嵼偟傑偡丅
廬偭偰丄恀嬻偼壗傕柍偄嬻娫偱偼側偔丄幚懱偑懚嵼偟偰偄傑偡丅廬偭偰丄偁傜備傞姷惈宯偐傜偁傜備傞姷惈宯偵丄摨堦曄姺幃偱
曄姺媦傃媡曄姺弌棃傞昁梫偼偁傝傑偣傫丅
丂傑偨丄揹帴攇偺憡懳懍搙偼晄曄偱偼偁傝傑偣傫丅儅僢僋僗僂僃儖偺曽掱幃偑偁傜備傞姷惈宯偱巊偊傞偺偼丄揹帴攇偺憡懳懍搙
偑晄曄偱偁傞偐傜偱偼側偔丄棻巕娫偺墲暅嫍棧偑丄忢偵惷巭帪偲摨偠偲側傞條偵丄偍屳偄偺憡懳嫍棧偑廂弅偡傞偐傜偱偡丅
偦偆側傞偲丄揹帴攇偼堏摦懍搙v偵娭傢傜偢丄忢偵墲暅嫍棧偼摨偠偲側傝丄嫍棧偺2忔偵斀斾椺偡傞揹帴攇偺椡偼丄堏摦偡傞姷惈宯偱傕
惷巭帪偲摨抣側偺偱偡丅
丂偟偐偟丄堦乆揹帴攇偺憡懳懍搙偲棻巕娫偺嫍棧偺曄壔傪寁嶼偡傞偙偲偼崲擄偱偡丅寁嶼寢壥偼摨偠側偺偱丄偄偭偦偺偙偲丄岝偺憡懳懍搙
偲棻巕娫偺嫍棧偼曄壔偟側偄偲壖掕偟偰丄堏摦偡傞姷惈宯偱偦偺傑傑儅僢僋僗僂僃儖偺曽掱幃傪巊偭偰寁嶼偟偨曽偑曋棙偱偡丅
偦偆壖掕偟偰寁嶼偟偰傕丄偦偺寢壥捠傝偵暔棟尰徾偼恑峴偡傞偐傜偱偡丅偙傟偑丄乽岝懍搙晄曄偺梫惪乿偱偁傝丄尰幚偲偼堎側傝傑偡偑丄
曄姺屻偺岝偼忢偵c偱偁傞昁梫偑偁傞偺偱偡丅儘乕儗儞僣曄姺偼丄偙偺梫惪傪姰慡偵枮偨偟傑偡丅
傑偨丄惷巭宯丒塣摦偡傞姷惈宯偺嬫暘側偔丄曄姺媦傃媡曄姺弌棃傑偡丅
5.媡曄姺弌棃傞梫審
丂儘乕儗儞僣曄姺偼丄乽岝懍搙晄曄偺梫惪乿偲乽媡曄姺偑壜擻偱偁傞偙偲乿偺俀偮偺梫惪偺傒偐傜摫偐傟偨悢幃偱偟傚偆偐丅
娤應幰偑X幉曽岦傊懍搙v偱堏摦偟側偑傜丄岝傪娤應偡傞偲尵偆忦審偺傒傪丄壖掕偟偰乽岝懍搙晄曄偺朄懃乿偲
乽媡曄姺乿偑壜擻側悢幃偺昁梫廫暘忦審傪挷傋偰尒傑偡丅
嘆x'=x-vt丂乮娤應幰偑X幉曽岦傊懍搙v偱t昩娫堏摦偟偨偺偱丄岝偺X幉曽岦偺堏摦嫍棧偼偦偺暘彮側偔娤應偝傟傞乯
嘇y'=y丂丂丂乮娤應幰偑丄X幉曽岦傊懍搙v偱t昩娫堏摦偟偰傕丄岝偺Y幉曽岦偺堏摦嫍棧偼曄壔偟側偄乯
嘊z'=z丂丂丂乮娤應幰偑丄X幉曽岦傊懍搙v偱t昩娫堏摦偟偰傕丄岝偺Z幉曽岦偺堏摦嫍棧偼曄壔偟側偄乯
偺傒壖掕偟傑偡丅
丂偡傞偲岝懍搙偑晄曄偵側傞堊偵帪娫倲偺曄姺幃偼
t'=t*(併乮c2-2vccos兤+v2乯/c )
偲側傝傑偡丅
丂ctcos兤=x丂偱偡偺偱丄
嘋t'=t*(併乮c2-(2vx)/t+v2乯/c )
偱偡丅嘆偐傜嘋傪婎杮曄姺幃偲屇傃傑偡
6.婎杮曄姺幃偱媡曄姺弌棃傞偐
丂偙偺婎杮曄姺幃偑丄惓曄姺偱岝懍搙晄曄偺梫媮傪枮懌偡傞偐丄挷傋傑偡丅
嘍x2+y2+z2=c2*t2
偱偡丅
嘐x'2+y'2+z'2=c2*t'2
偲側傞偐挷傋傑偡丅
嵍曈=(x-vt)2+y2+z2=x2-2vtx+v2*t2+ y2+z2
塃曈= c2*t2*(c2-(2vx)/t+v2)/c2)= t2*(c2-(2vx)/t+v2))= c2*t2-2vtx+ v2*t2
-2vtx+v2*t2偺晹暘偼摍偟偔徚偊傑偡偺偱丄巆傞偺偼
嘍x2+y2+z2=c2*t2
偲側傝丄嘐偑忢偵惉棫偟乽岝懍搙晄曄偺梫惪乿傪枮懌偟傑偡丅
丂崱搙偼丄婎杮曄姺幃偱丄媡曄姺偑弌棃傞偐挷傋偰傒傑偡丅
丂媡曄姺幃偼丄v傪-v偵偟丄(x,y,z,t)傪(x',y',z',t')偵偟傑偡丅
嘑x=x'+vt'
嘒y=y'
嘓z=z'
嘔t=t'*(併乮c2+(2vx')/t'+v2乯/c )
偲側傝傑偡丅崱
嘐x'2+y'2+z'2=c2*t'2
偼惉棫偟偰偄傑偡丅偦偙偱丄
嘍x2+y2+z2=c2*t2
偑惉棫偡傞偐挷傋偰傒傑偡丅
嵍曈=(x'+vt')2+y'2+z'2=x'2+2vt'x'+v2*t'2+ y'2+z'2
塃曈= c2*t'2*(c2+(2vx')/t'+v2)/c2)= t'2*(c2+(2vx')/t'+v2))= c2*t'2+2vt'x'+ v2*t'2
2vt'x'+v2*t'2偺晹暘偑摍偟偔徚偊傑偡偺偱丄巆傞偺偼
嘐x'2+y'2+z'2=c2*t'2
偲側傝傑偡丅嘍偼忢偵惉棫偟丄婎杮曄姺幃偱媡曄姺傪峴偭偰傕丄乽岝懍搙晄曄偺梫惪乿傪枮懌偟傑偡丅
7.恾夝
丂偙偺偙偲傪丄恾偱昞尰偡傞偲師偺捠傝偲側傝傑偡丅
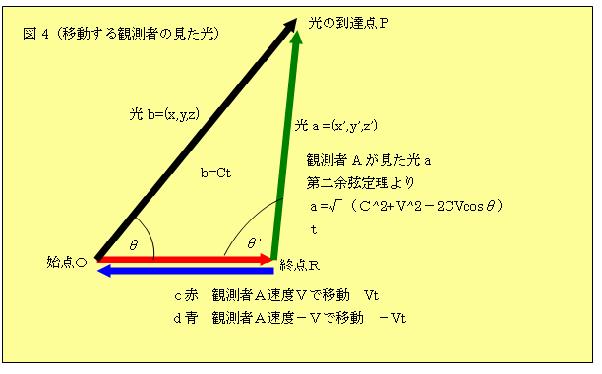 丂娤應幰乮愒栴報乯偐傜尒偨岝倐偼岝倎偲娤應偝傟傑偡丅偮傑傝娤應幰偑懍搙v偱堏摦偡傞偲丄岝倐(ct)偼戞擇梋尫掕棟偵傛傝丄
岝倎(併乮c2+v2-(2vx)/t乯)偵曄姺偝傟傑偡丅帪娫t傕併乮c2-(2vx)/t +v2乯/c偵曄姺偝傟傞堊乮岝倐偺傒偱側偔丄
O仺P曽岦傊揱傢傞4偮偺椡偼慡偰摨條偺曄壔傪偟偰偄傞偺偱丄偦偺曽岦傊偼係偮偺椡偑揱傢傞偺偵梫偡傞帪娫偼
倲'=t*併乮c2+v2-2cvcos兤乯/c偲曄壔偟偰偄傑偡丅偮傑傝丄偦傟偩偗暔幙帪娫偼曄壔偟偰偄傑偡乯丄岝懍搙偼堦掕偱偡丅
丂娤應幰乮愒栴報乯偐傜尒偨岝倐偼岝倎偲娤應偝傟傑偡丅偮傑傝娤應幰偑懍搙v偱堏摦偡傞偲丄岝倐(ct)偼戞擇梋尫掕棟偵傛傝丄
岝倎(併乮c2+v2-(2vx)/t乯)偵曄姺偝傟傑偡丅帪娫t傕併乮c2-(2vx)/t +v2乯/c偵曄姺偝傟傞堊乮岝倐偺傒偱側偔丄
O仺P曽岦傊揱傢傞4偮偺椡偼慡偰摨條偺曄壔傪偟偰偄傞偺偱丄偦偺曽岦傊偼係偮偺椡偑揱傢傞偺偵梫偡傞帪娫偼
倲'=t*併乮c2+v2-2cvcos兤乯/c偲曄壔偟偰偄傑偡丅偮傑傝丄偦傟偩偗暔幙帪娫偼曄壔偟偰偄傑偡乯丄岝懍搙偼堦掕偱偡丅
丂崱搙偼媡偵丄娤應幰乮惵栴報乯偑岝倎傪懍搙-v偱堏摦偟側偑傜娤應偡傞偲丄岝倎偼戞擇梋尫掕棟偵傛傝丄尦偺岝倐偵曄姺偝傟傑偡丅
帪娫傕摨偠妱崌偱曄壔偟乮峫偊曽偼忋婰偲摨條乯丄岝懍搙晄曄偺梫媮傪枮懌偟傑偡丅惓曄姺偲媡曄姺偼丄
婎杮曄姺幃偱帺嵼偵弌棃傑偡丅
8.儘乕儗儞僣偑暘曣傪併(1-v2/c2)偲偟偨棟桼
丂廬偭偰丄乽岝懍搙晄曄偺朄懃乿偲乽媡曄姺乿偑壜擻側悢幃傪媮傔傞偩偗偱偁傟偽丄婎杮曄姺幃偱昁梫廫暘偱偁傝丄
儘乕儗儞僣曄姺偺條偵丄帪娫倲媦傃恑峴曽岦偱偁傞師尦倶偺曄姺幃偺暘曣偑併(1-v2/c2)偲側傞昁梫偼慡偔偁傝傑偣傫丅
偦傟偵偼丄傕偭偲懠偺堄枴偑偁傞條偱偡丅
丂儘乕儗儞僣偼丄乽僄乕僥儖乿傪惷巭宯偲峫偊傑偟偨丅儘乕儗儞僣偼丄堏摦偟偨応崌丄暔幙偼僄乕僥儖偺掞峈傪惓柺偐傜庴偗傞偺偱丄
恑峴曽岦傊併乮1-v2/c2乯廂弅偡傞偲峫偊傑偟偨丅偙傟傪儘乕儗儞僣廂弅偲尵偄傑偡丅
丂Y幉傗Z幉曽岦偼乽僄乕僥儖乿偺掞峈傪庴偗側偄偺偱丄偦偺曽岦傊偼暔幙偼廂弅偟傑偣傫丅
丂偙偺儘乕儗儞僣廂弅偵傛傝丄儅僀働儖僜儞偲儌乕儗乕偺幚尡憰抲偼丄恑峴曽岦傊併乮1-v2/c2乯廂弅偟丄
廲曽岦偺墲暅嫍棧=墶曽岦偺墲暅嫍棧=11/併乮1-v2/c2乯倣
偲側傞堊丄岝偼摨帪偵栠傞偙偲偑弌棃偨偲峫偊傑偟偨丅
丂婎杮曄姺幃偺t偲x偺曄姺幃偺暘曣偵乮1-v2/c2乯傪晅偗傞偲丄儘乕儗儞僣曄姺偵側傝傑偡丅偦偟偰丄
晅偗壛偊偰傕丄媡曄姺偺弌棃傞幃偲側偭偰偄傑偡丅
9.暘曣偑併(1-v2/c2)偲側傞恀偺棟桼
丂戞堦曄姺偲戞嶰曄姺傪摑崌偡傞偲丄
t'=t/併乮1-v2/c2乯
x'=x/併乮1-v2/c2乯
y'=y
z'=z
偲側傝傑偡(戞堦曄姺偲戞嶰曄姺偺徻嵶偼僩僢僾儁乕僕傪嶲徠壓偝偄)丅廬偭偰丄曄姺偵偼婎杮曄姺幃偺傒偱偼懌傝偢丄
t偲x偺暘曣偵併乮1-v2/c2乯傪壛偊傞昁梫偑偁傞偺偱偡丅

 丂娤應幰乮愒栴報乯偐傜尒偨岝倐偼岝倎偲娤應偝傟傑偡丅偮傑傝娤應幰偑懍搙v偱堏摦偡傞偲丄岝倐(ct)偼戞擇梋尫掕棟偵傛傝丄
岝倎(併乮c2+v2-(2vx)/t乯)偵曄姺偝傟傑偡丅帪娫t傕併乮c2-(2vx)/t +v2乯/c偵曄姺偝傟傞堊乮岝倐偺傒偱側偔丄
O仺P曽岦傊揱傢傞4偮偺椡偼慡偰摨條偺曄壔傪偟偰偄傞偺偱丄偦偺曽岦傊偼係偮偺椡偑揱傢傞偺偵梫偡傞帪娫偼
倲'=t*併乮c2+v2-2cvcos兤乯/c偲曄壔偟偰偄傑偡丅偮傑傝丄偦傟偩偗暔幙帪娫偼曄壔偟偰偄傑偡乯丄岝懍搙偼堦掕偱偡丅
丂娤應幰乮愒栴報乯偐傜尒偨岝倐偼岝倎偲娤應偝傟傑偡丅偮傑傝娤應幰偑懍搙v偱堏摦偡傞偲丄岝倐(ct)偼戞擇梋尫掕棟偵傛傝丄
岝倎(併乮c2+v2-(2vx)/t乯)偵曄姺偝傟傑偡丅帪娫t傕併乮c2-(2vx)/t +v2乯/c偵曄姺偝傟傞堊乮岝倐偺傒偱側偔丄
O仺P曽岦傊揱傢傞4偮偺椡偼慡偰摨條偺曄壔傪偟偰偄傞偺偱丄偦偺曽岦傊偼係偮偺椡偑揱傢傞偺偵梫偡傞帪娫偼
倲'=t*併乮c2+v2-2cvcos兤乯/c偲曄壔偟偰偄傑偡丅偮傑傝丄偦傟偩偗暔幙帪娫偼曄壔偟偰偄傑偡乯丄岝懍搙偼堦掕偱偡丅