★第一部光速度　 近日点の移動 マックスゥエル マイケルソンとモーレー 光行差 c-vcosθ 物質収縮 自然哲学 物質変化 静止系 光速度不変の要請 逆変換 レーザー 速度の加法則 横ドップラー 時空間の変化 ローレンツ収縮 リングレーザージャイロ 同時性の相対性 ウラシマ効果 物質波

光速度は不変ではなく(c-vcosθ)キロメートル/秒と観測される

　ロケットの自動操縦に使われるリングレーザージャイロ装置において、光の速度を(c-vcosθ)キロメートル/秒 と設定している。

1.光の相対速度は√(c2+v2-2vccosθ)[m/s]である

v慣性系に於ける光の速度 　Ⅰ.観測者はOR移動し、光はOP進む。観測者には光がRP進んだと観測される。光の速度はc[m/s]、観測者の速度はv[m/s]なので、 光の相対速度は、第二余弦定理より
RP=√(c2+v2-2cvcosθ)[m/s]
と導くことが出来る。
　この変化は
ア　t'=t
イ　x'=x-vｔ
ウ　y'=y
エ　z'=z
オ　c'=√(c2+v2-2cv*cosθ)
と表される。
　※(x,y,z)=(ct*cosθ,ct*sinθ,0)の平面で考えると、
√{(x'2+y'2+z'2)=√(ct*cosθ-vｔ)2+ (ct*sinθ)2+02}=t*√(c2+v2-2cv*cosθ)=c't
　∴c'=√(c2+v2-2cv*cosθ)
目次へ

2.空間の定義の変化

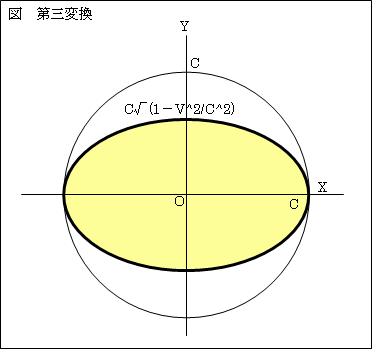第三変換 　Ⅰ.高速移動に伴う物質の収縮により、空間は
カ　t'=t
キ　x'=x
ク　y'=y*√(1-v2/c2)
ケ　z'=z*√(1-v2/c2)
と変換される(太線に変換される)。空間は縦に√(1-v2/c2)収縮する。
　以下において、その変化を説明する。
目次へ

3．物質の大きさを決める要素

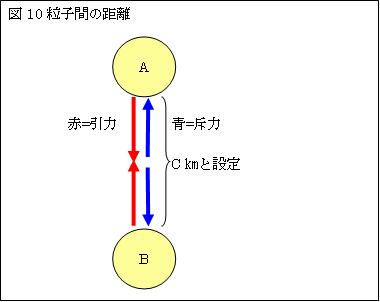粒子間の距離 　Ⅰ.物質を構成する粒子と粒子とは、互いに接し合っているのではない。一定距離を保っている。 何故、粒子同士は一定距離を保っているのか。
　物質を構成する粒子と粒子間には、引力と斥力とが働いている。引力と斥力は光速c[m/s]で伝わる。 その引力と斥力の釣り合う一定距離を保っている。
　(説明を簡単にする為に、ここでは、L=c[m]と設定している。)
目次へ

4．物質が収縮する仕組み

収縮する仕組み

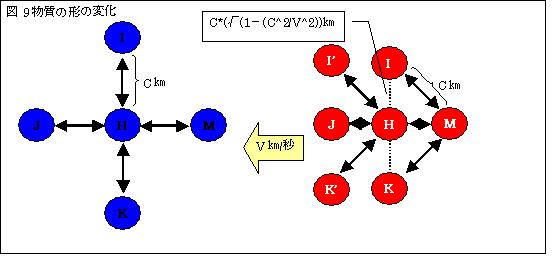
　Ⅰ.青は、物質が静止している状態である。IとHは引力と斥力とが釣合い、一定距離を保っている。その距離を便宜上c[m]とする。 引力と斥力は1秒間で到達する。
　物質が速度v[m/s]で、左へ移動したとする。 速度vで移動する慣性系において、物質を動かす4つの力の相対速度は、
√（c2+v2-2cvcosθ）[m/s]
となる。赤のIHは、進行方向とは90°の角度の位置にあるので、HからIへ（往路）はcosθ=v/cである。よって、4つの力の速度は、
√（c2+v2-2v2）=√（c2-v2）[m/s]
である。IからHへ（復路）伝わる4つの力の速度も同値である。

　従って、HI間がc[m]とすると、往路に要する時間は、c/√（c2-v2)秒である。 IH間の復路も同じ時間掛かる。往復2秒の位置で、 引力と斥力は釣り合うので、釣り合う距離は
2秒/(2c/√（c2-v2))秒=√(1-v2/c2)倍
に収縮する。

　Ⅱ.進行方向である、赤のJH間では、HからJへの往路はcosθ=1、JからHへの復路はcosθ=-1である。 従って4つの力の伝わる速度は、
HJ間(往路)=√（c2+v2-2cv）=(c-v)[m/s]
JH間（復路)=√（c2+v2+2cv）=(c+v)[m/s]
　HJ間をc[m]とすると、往路に要する時間は、
c/(c-v)秒
　復路に要する時間は、
c/(c+v)秒
合計で、
c/(c-v)+c/(c+v)=2c2/(c2-v2)秒
掛かる。往復2秒の位置で、引力と斥力は釣り合うので、釣り合う距離は
2/(2c2/(c2-v2))=(1-v2/c2)倍
となる。
　従って、高速移動すると物質は、縦に√(1-v2/c2)、横に(1-v2/c2) 収縮する。
目次へ

5．マイケルソンとモーレーの実験

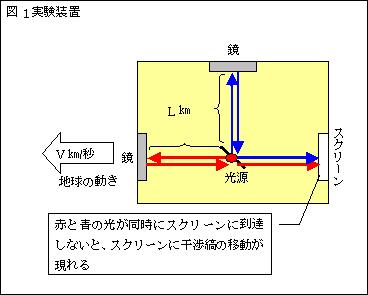マイケルソンとモーレーの実験 　Ⅰ.マイケルソンとモーレーは、光はエーテルを伝わる波であることを証明する為に、次の様な実験を行った。
　鏡を使い光を縦方向と横方向に片道11メートルの距離を往復させて、同時に戻るか調べた。
　光の相対速度は、√(c2+v2-2cvcosθ)[m/s]である。縦方向はcosθ=v/cなのでその速度は、 √(c2-v2)[m/s]であり、往復22ｍ移動するには
22/√(c2-v2)千分の一秒掛かり、光の絶対速度はc[m/s]なので、その実際の距離は
縦方向の往復距離=22c/√(c2-v2)=22/√(1-v2/c2)ｍ
となる。

　Ⅱ.横方向の往路はcosθ=1、復路はcosθ=-1なので
往路の光の相対速度=(c-v)[m/s]
復路の光の相対速度=(c+v)[m/s]
　従って
往路に要する時間=11/(c-v)千分の一秒
復路に要する時間=11/(c+v)千分の一秒
　合計で
往復に要する時間=11/(c-v)+11/(c+v)=22/(c2-v2)千分の一秒
となる。光の絶対速度はc[m/s]なので、その実際の距離は
横方向の往復距離=22c/(c2-v2)=22/(1-v2/c2)ｍ
となる。

　Ⅲ.この様に縦方向と横方向の往復距離は異なる為、光は同時には戻れないと思われる。
　しかし、物質を構成する粒子間の距離は、
縦方向へ√(1-v2/c2)倍
横方向へ(1-v2/c2)倍
収縮する。この収縮により
縦方向の往復距離=22*√(1-v2/c2)/√(1-v2/c2)=22ｍ
横方向の往復距離=22*(1-v2/c2)/(1-v2/c2)=22ｍ
と静止時と同じとなり、光は常に同時に戻ることが出来る。
目次へ

6．実験装置を単純化する

実験装置

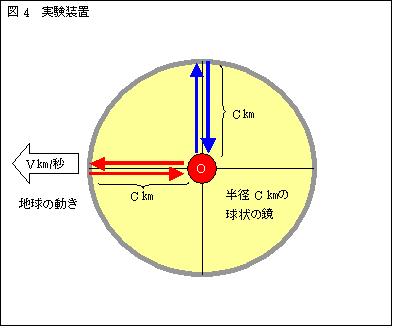
　Ⅰ.考え方を単純にする為に、左の様な装置に変える。半径c[m]の球体の鏡を想定する。光源Oから青い光と赤い光が同時に出発し、 半径c[m]（299,792.5[km]）の球形の鏡に反射して再びOに戻る。

　Ⅱ.装置は、左に速度v[m/s]で移動している。実験の結果、鏡がvで移動しているにもかかわらず、Oを出発した全ての方向の光は、 同時にOに戻った。
目次へ

7．実際に光が移動した軌跡を調べる

光の軌跡

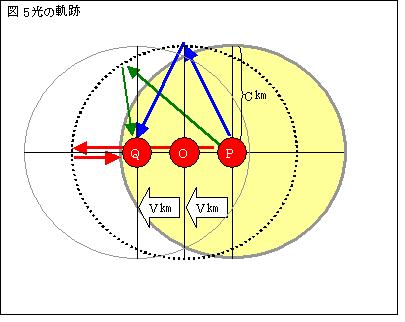
　Ⅰ.光源Pが、速度v[m/s]でQに移動した。Pから発せられた、あらゆる方向の光は、鏡(M)に反射されて、同時にQに到達した。 光の絶対速度は全てc[m/s]である。

　∴全ての光が移動した距離は同じである。点線の位置で反射したとする。この点線は、 点PとQを2つの焦点とする楕円となる。
目次へ

8．光の反射点を結ぶと楕円となる

点線の形

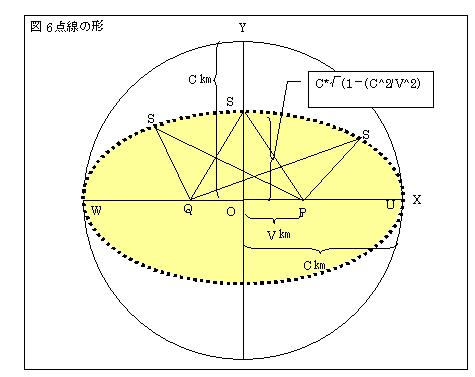
　Ⅰ.楕円上の任意の点をSとする。静止時では、光の往復距離は2c[m]で、それに要する時間は2秒であった。
　光の往復距離が、PS+QS=2cとなる楕円は、
X2/c2+Y2/(c2-v2)=1
である。OP=v、OQ=-v、OU=c、OW=-c、なので、
楕円の離心率(OP/OU)=(√(c2-(c2-v2)))/c= v/c
焦点(OPとOQ)=c* v/c=v、c* (-v/c)=-v
焦点PとQと楕円上の点Sを結ぶ距離(PS+QS)=2c
で、それが正しいことが分かる。※公式より

　Ⅱ.この楕円は、静止時における球形の鏡M（実線の円）である、
X2+Y2=c2
をX'=X、Y'=(√(c2-v2)/c)*Y=(√(1-v2/c2)*Y
に変換したものである。※公式より

　Ⅲ.つまり、円(鏡M)を縦方向に、√(1-v2/c2)倍に収縮した形となる。 全ての光は、この楕円上の点線位置で反射している。P→S→Qの距離は、Sが楕円上のどの位置であっても2cとなる。 光がP→S→Qの距離を移動するのに要する時間は2秒であり、静止時と変わらない。

目次へ

9．空間の定義は縦に√(1-v2/c2)収縮する

　Ⅰ.移動する観測者は、同時に出発した光が同時に返ってくる楕円を円と定義する。これを静止者が見ると楕円と見える。 従って、移動系では空間が縦に√(1-v2/c2)収縮されて定義され、上記2.空間の定義の変化の変換式の通りとなる。
目次へ

10.光行差のブラッドリーの方程式は、空間が縦に√(1-v2/c2)収縮した時成立する

　Ⅰ.星を望遠鏡で見る場合、実際に星のある方向に望遠鏡を向けても、その星は見えないことが知られている。 少し地球の進行方向に望遠鏡を傾けてやらないと、その星は見えない。

光行差

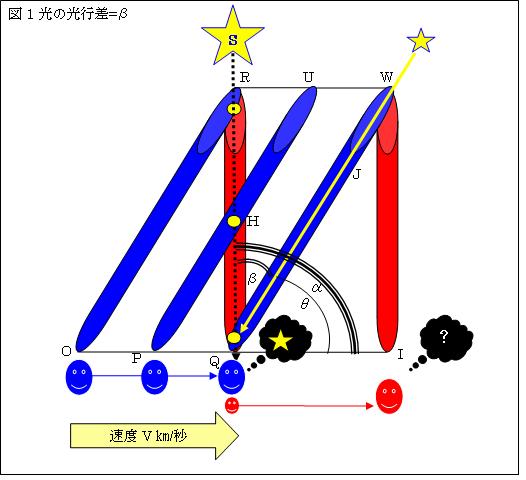
　Ⅱ.例えば、赤い観測者が真っ直ぐ星Sに望遠鏡を向けても、望遠鏡は地球の動きと共にIに動くので、星Sからの光は、 望遠鏡の筒を通り抜けることが出来ず、赤い観測者に星は見えない。

　Ⅲ.青い観測者の様に、地球の進行方向へβだけ望遠鏡の筒を傾けてやると、星Sからの光は、R→H→Qと上手に筒を通り抜けて、 青い観測者は星を見ることが出来る。このβを光行差と言う。

　Ⅳ.この光行差は、ブラッドリーの式
sinβ=(v/c)sinα
として表わされる。

目次へ

11.各区間の距離の設定

各部分間の距離

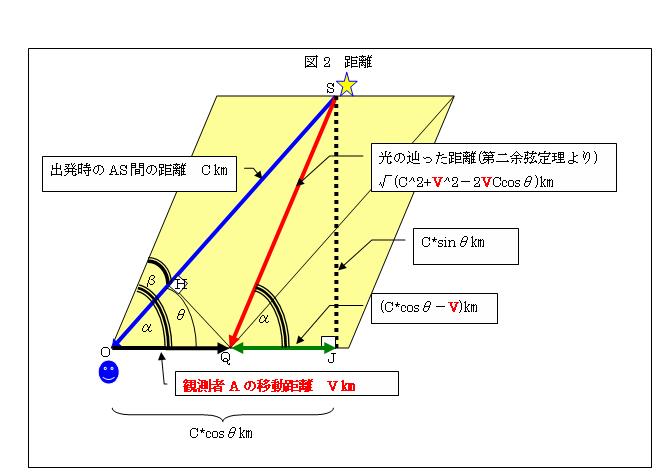
　Ⅰ.説明を単純にする為に、z=0の平面で説明する。出発点Oにおける青い観測者Aと、星Sとの距離をc[m]とする。 そして、望遠鏡もOS=c[m]とする。青い観測者は、Q地点で望遠鏡の筒を通って来た星Sからの光を見ることが出来る。 SからOQの延長線上に垂線を下ろし、その点をJとする。各区間の距離を図2の通り設定する。

　Ⅱ.OS間はc[m]である。
Oを出発して1秒後に観測者Aは、Qに到達する。従ってOQ=v[m]である。
　その時、Aは星Sから来た光を望遠鏡で見る。 SQは第二余弦定理より、√(c2+v2-2vccosθ)[m]である。
SJ=c*sinθ[m]である。
OJ=c*cosθ[m]なので、QJ=(c*cosθ-v)[m]である。

目次へ

12.ブラッドリーの式の導出

　Ⅰ.sinα= c*sinθ/√(c2+v2-2vccosθ)
sinβ= sin(α-θ)= sinα*cosθ-cosα*sinθ　(公式より)
= (c*sinθ/√(c2+v2-2vccosθ))* cosθ-((c*cosθ-v)/ √(c2+v2-2vccosθ))* sinθ
= (sinθ/√(c2+v2-2vccosθ))*(c* cosθ-c*cosθ+v)= v* sinθ/ √(c2+v2-2vccosθ)
∴sinβ=(v/c)sinα
と、ブラッドリーの式が導かれる。望遠鏡はβだけ進行方向へ傾いている。

　Ⅱ.しかし、この距離設定は、常識的に考えるとおかしな点があります。Aはvキロメートル/秒でOQ移動した。 OQ=vキロメートルなので、光は1秒かけてSQを進みAに到達した。光の絶対速度はcキロメートル/秒なので、SQ=cのはずである。

　Ⅲ.それが、ブラッドリーの式では、SQ=√(c2+v2-2cv*cosθ)と設定されている。 つまり進行方向は距離設定に変化はないが、縦方向には空間が収縮した様に設定されてる。


目次へ

13.空間が縦に√(1-v2/c2)収縮すれば矛盾は解消される

　Ⅰ.収縮する前の星の位置をS'とし、S'から下ろした垂線の足をJ'とし、SからS'J'に下ろした垂線の足をRとする。
　縦方向には、S'J'がRJ'に収縮した。S'J'=c*sinα、RJ'=√(c2+v2-2cv*cosθ) *sinαなので、
縦方向の収縮率=√(c2+v2-2cv*cosθ)/ c
である。垂直方向は、cosθ=v/cなので、
収縮率=√(c2-v2)/c=√(1-v2/c2)
である。

　Ⅱ.従って、高速移動に伴い時空間は、
カ　t'=t
キ　x'=x
ク　y'=y*√(1-v2/c2)
ケ　z'=z*√(1-v2/c2)
と変換されている。この様に、ブラッドリーの式からは、 高速運動により空間が縦方向へ√(1-v2/c2)収縮した様に観測されることが分かる。
目次へ

14.光の相対速度c-vcosθの導出

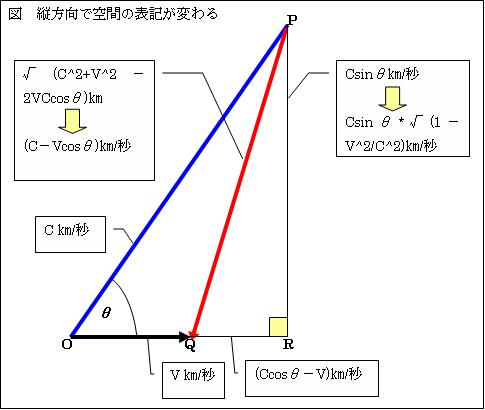ビジュアル的表示 　Ⅰ.光の相対速度√(c2+v2-2cv*cosθ)[m/s]を、カからケの変換式を用いて変換して見る。

　c[m/s]で進む光OPは、観測者Aが速度v[m/s]でOQ移動する為、AにはQP進んだと見える。第二余弦定理より、 QP=√(c2+v2-2cv*cosθ)[m/s]と光の相対速度が導かれる。
PQ=√(QR2+PR2) =√{(ccosθ-v)2+(csinθ)2} =√(c2cosθ2-2cvcosθ+v2+c2sinθ2) =√(c2+v2-2cvcosθ)[m/s] である。

　Ⅱ.カからケの変換では、縦方向の空間が√（1-v2/c2)短く表記される。PR=csinθ[m/s]であったのが、 第三変換により、PR=csinθ*√（1-v2/c2)[m/s]と表記される。横方向の表記は変わらないので、 QR=(ccosθ-v)[m/s]のままである。


　Ⅲ.変換後のPQ=√(QR2+変換後のPR2) =√{(ccosθ-v)2+{csinθ*√（1-v2/c2)}2}
=√（1-v2/c2)*√{{(ccosθ-v)/√（1-v2/c2)}2+(csinθ)2}
=√（1-v2/c2)*c*√{(c2cosθ2-2cvcosθ+v2)/(c2-v2)}+sinθ2}
=√（1-v2/c2)*c*√{(c2cosθ2-2cvcosθ+v2+c2sinθ2-v2sinθ2)/(c2-v2)}
={√（1-v2/c2)/√{（1-v2/c2)}*√{c2(cosθ2+sinθ2)-2cvcosθ+v2-v2(1-cosθ2)}
=√(c2-2cvcosθ+v2cosθ2)
=√(c-vcosθ)2=(c-vcosθ)[m/s]
となり、光の相対速度(c-vcosθ)[m/s]が導かれる。
目次へ

15.実際に観測される光の速度

リングレーザージャイロ装置 　Ⅰ.この宇宙で実際に観測される光の速度は、上記の通り、(c-vcosθ)[m/s]です。ロケットの自動操縦に使用するリングレーザージャイロ装置において、 光の速度を(c-v*cosθ)[m/s]と設定していることからも、正しいことが分かる。

　Ⅱ.光ファイバーの輪の中を、青い光は左回りに、赤い光は右回りに移動している。装置自体が右へOからPへ回転移動した状態を考える。 観測者Aは、OからPへ移動する。Oを同時に出発した青い光と赤い光は、Pの位置で観測者Aに出会う。青い光は左回りにO→P進む。 赤い光は右回りにO→O→P進む。
　青青い光と赤い光が、Pに到達する時間の差を測定することにより、 リングレーザージャイロ装置自体が、どれだけ回転運動をしたのか計算することが出来る。これにより、 ロケットは一定方向へ軌道修正しながら進むことが出来る。

　Ⅲ.この装置では、光の相対速度は(c-vcosθ)キロメートル/秒として、装置の回転を計算している。 つまり、O→Pの運動をvキロメートル/秒とすると、進行方向へはcosθ=1、逆方向へはcosθ=-1なので、 赤い光の相対速度は(c-v)キロメートル/秒、青い光の相対速度は(c+v)キロメートル/秒と計算される。 双方の差は2vキロメートル/秒なので、vキロメートル/秒分逆方向へ回転すると、ロケットは真っ直ぐに進むことが出来る。

目次へ

16.光速度不変の要請

　Ⅰ.では何故ローレンツ変換は、事実とは異なる「光速度不変」を仮定しているのか。
　電磁力は電荷を帯びた物質が光である電磁波を交換することで生じる。物質が移動しながら電磁波を交換すると、 電磁波の往復距離は、縦に1/√(1-v2/c2)、横に1/(1-v2/c2)伸びる。 従って、移動系では生じる電磁力が弱まると思われる。

　Ⅱ.しかし、マックスウェルの方程式では、真空の誘電率と誘磁率を定数としており、 静止系でも移動系でも生じる電磁力の強さは変わらないとしている。

　Ⅲ.この矛盾を解消するものに、「光速度不変の原理」がある。物質が移動しても、その間を行き来する電磁波(光)の相対速度 は不変であり、電磁波の往復に要する時間は同じなので、移動系でも静止系と同じ強さの電磁力が生じるとする。
　しかし、リングレーザージャイロ装置の実例から分る通り、それは真実ではない。

　Ⅳ.もう１つの解法として、上記の通り移動系では物質は、縦に√(1-v2/c2)、 横に(1-v2/c2)収縮すると考える。これで、移動系でも電磁波(光)の往復距離は不変となり、 移動系でも静止系でも生じる電磁力の強さは同じとなる。

　Ⅴ.ローレンツ収縮は、物質は進行方向(横に)に√(1-v2/c2)収縮すると解する。しかし、これでは
縦方向の電磁波の往復距離=2c/√(1-v2/c2)[m]
横方向の電磁波の往復距離= 2c√(1-v2/c2)/(1-v2/c2)= 2c/√(1-v2/c2)[m]
となり、マイケルソンとモーレーの実験結果を説明することは出来ても、電磁波の往復距離は速度vにより変化する為、 移動系では生じる電磁力の強さが弱まる。これでは、マックスウェルの方程式の方程式が、移動系でも使えることを説明することは出来ない。

　 　Ⅵ.真実通り、電磁波の相対速度と粒子間の距離の収縮を一々計算して、 物質間に生じる電磁力の強さを計算することは大変困難である。結果が同じなら、光速度と粒子間の距離を不変と仮定して、 簡単に計算出来るローレンツ変換を使用すべきである。 これが「光速度不変の要請」である。

　Ⅶ.ローレンツ変換は、事実とは異なる「光速度不変」を仮定することにより、物理計算を可能なものとしている。この意味において、 ローレンツ変換は画期的な発明である。
　ローレンツ変換を基礎とする特殊相対性理論においても、「光速度不変」を仮定することにより、 計算を可能なものにし、様々な方程式を導いている。そして、あらゆる試験をパスして来た。
　しかし、特殊相対性理論において、時間の変換を計算する際は、ローレンツ変換
t'= (t-(vx/c2)) / √（1-v2/c2)
とは異なり、
t'=t/√（1-v2/c2）
を使用している。そうすると
√(x'2+y'2+z'2)=(c-v cosθ)*t/ √（1-v2/c2)=c't'
なので
c'=c-vcosθ
でなくてはならなくなる。このことからも「光速度不変」は、計算を簡便にする為の要請であることが分る。