惑星は何故、楕円軌道を回るのか(ケプラーの第一法則)

�T.惑星の軌道半径と公転速度の関係

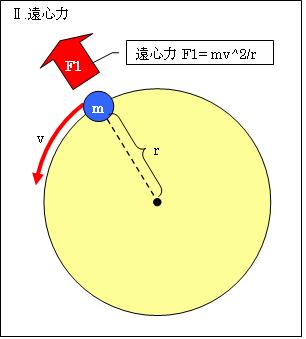
　先ず、惑星の公転軌道を円で説明します。その後、公転軌道が楕円となる仕組みを説明します。

　惑星は太陽の周りを回ることにより、遠心力を受け外に飛び出そうとします。

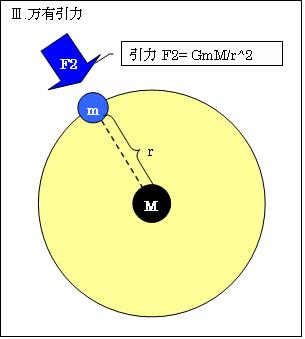　また、惑星は太陽の万有引力により引かれます。
　その、遠心力と太陽の万有引力が釣り合う一定軌道を惑星は公転しています。つまり、双方の力が釣り合うには、惑星の軌道半径と惑星の公転速度の間に一定の関係が必要となります。

�@遠心力F=mv²/r　 (m=惑星の質量[�s]、v=惑星の公転速度[m/s]、r=惑星の公転半径[m])
�A万有引力F’=GMm/r²　(G万有引力定数=6.67408×10^-11[m³�s^-1s^-2]、M=太陽の質量[�s]、m=惑星の質量[�s]、r=惑星の公転半径[m])
です。

�U.ケプラーの第二法則(面積速度一定の法則)

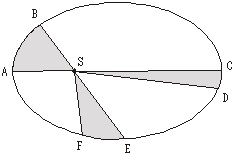
　次にケプラーの第二法則に移ります。

　惑星が同じ時間に弧AB・弧CD・弧EF動きます。すると、扇形ABS・扇形CDS・扇形EFSの面積が等しくなります。
　これを「太陽と惑星が一定時間に移動した軌道を結ぶ扇形の面積Sは一定である」と言います。

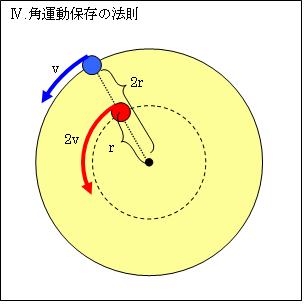　これは「角運動量保存の法則」から導くことが出来ます。

�B角運動量a=mrv　(m=回る物質の質量・r=回転する円の半径・v=回転速度)
です。この運動量aが一定になります。

　つまり、惑星の公転半径を半分にすると回転速度は2倍になります。これで
角運動量=m×r/2×2v=mrv=一定
となります。

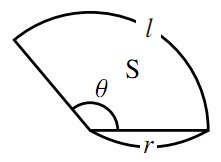　扇形の面積S=半径r×弧の長さl÷2です。一定時間の弧の長さl=惑星の速度v×時間t=vtです。

したがって
S=r×vt÷2= rat/2mr=at/2m
です。a=一定値、t=一定時間、m=惑星の質量(不変)なので、扇形の面積Sは不変となります。

�V.ケプラーの第一法則(楕円軌道の法則)

　しかし惑星は、太陽を1つの焦点とする楕円軌道を回っています。どうして惑星は楕円軌道を回るのでしょうか。

　今までの説明を整理します。完全な円軌道を公転する惑星は、遠心力Fと万有引力F’の釣り合う円軌道を回ります。

　※土星の輪を考えて下さい。完全な円形をしています。1つ1つの塵が楕円軌道を描こうとしても、お互いに万有引力により引き合っているので、自由には動けません。こうして、全ての塵の運動が統一されて、完全な円軌道を公転するようになります。
　この塵が集まって惑星が形成されました。ですから、形成当初惑星は円軌道を公転していました。

　ですから
�@遠心力F=mv²/r
�A万有引力F’=GMm/r²
F= F’です。

　しかし、宇宙空間は完全な真空ではありません。微小な塵が漂っています。ですから、惑星の公転速度は落ちます。すると「遠心力F=mv²/r」なので、遠心力は弱まります。一方「万有引力F’=GMm/r²」なので、万有引力は変化しません。したがって、遠心力<万有引力となり惑星は太陽に近づきます。

　すると、公転半径と公転速度は
�B角運動量a=mrv⇒rv=a/m⇒v=a/rm
の関係にあるので、お互いに反比例し変化します。つまり、公転半径が1/2倍になると公転速度は2倍になります。

　その時、万有引力と遠心力の力の差はどれだけでしょうか。

�@と�Bより
�B'遠心力F= mv²/r= m×(a/rm)²/r=a²/mr³
です。
※一般式は
遠心力F=m(v*sinθ)²/r
角運動量a=mrv*sinθ
です。

　したがって
v=a/mr*sinθ
なので
遠心力F= m{ (a/mr*sinθ)*sinθ}²/r=a²/mr³
と�B'と同じになります。

　一方
万有引力F’= GMm/r²
です。角運動量a・万有引力定数G・太陽の質量M・惑星の質量mは何れも変化しない一定値です。ですから
�@遠心力F= α/r³
�A万有引力F’= α/r²
と表現出来ます。つまりa²/m= GMm=αです。

�@のとおり公転する惑星に掛る遠心力は、軌道半径rの3乗に反比例します。遠心力は元々回転半径rに反比例し、速度の2乗に比例します。そして、惑星の公転速度は、回転半径rに反比例します。
ですから、公転半径が1/2になると遠心力は2倍となり、更に公転速度が2倍になり遠心力は4倍になります。この2つの効果を合わせると、遠心力=2倍×4倍=8倍=2³倍となります。
一方、万有引力は、�Aのとおり公転半径rの2乗に反比例します。

　したがって
�C惑星に掛る力=遠心力と万有引力の強さの差=(α/r³)−(α/r²)=α(1/r³)−α(1/r²)=α{(1/r³)−(1/r²)}
です。

�W.惑星が楕円軌道を回る仕組み

　今までの説明をまとめると、左図の様になります。
　中心に太陽Sがあります。その周りを緑の惑星が�@→�A→�B→�Cと公転しています。赤と青の境界の点線の部分が、丁度�C遠心力F1=�A万有引力となる位置です。これより半径rが小さい青の部分は、遠心力の方が万有引力よりも大きくなります。逆に、これより半径rが大きい赤の部分では、万有引力の方が遠心力よりも大きくなります。

　点線の位置で太陽と惑星の距離r=1とします(r=1となる点線の位置は、近日点3と遠日点1の中間ではなく、もっと太陽Sよりの位置となります)。r=1の点線の位置では、α/r³(遠心力)=α/r²(万有引力)=αで両者は同じです。
　そして、(S−3)間を0.9、(S−1)間を1.1とします(これは、軌道半径rが1よりも小さい時と1よりも大きい時の、遠心力と万有引力を説明する便宜上の値です)。青の部分では、α/(0.9³)＞α/(0.9²)なので、遠心力F＞万有引力F’です。赤の部分では、α/(1.1³)＜α/(1.1²)なので、遠心力F＜万有引力F’です。

　惑星が速度vで太陽Sの周りを回ります。惑星が点線部分を公転すると公転軌道は完全な円となります。遠心力と万有引力とが同じだからです。

　今度は、速度vの惑星は点線より大きな軌道を回っており、位置�@にあるとします。ここでは万有引力＞遠心力なので、惑星は太陽に向かって落下します。落下速度は次第に速くなります。

　そして、位置�Aに来たところで万有引力=遠心力となります。しかし、�@から�Aまで落下した勢いで、惑星は更に太陽に近づきます。そして、青の領域に入ります。青の部分では遠心力＞万有引力なので、惑星が太陽に近づく速度は次第に遅くなって行きます。

　そして、位置�Bに来た時、惑星の太陽への接近は止まります。この位置では、遠心力＞万有引力なので、惑星は外に飛び出そうとして太陽から遠ざかって行きます。遠ざかる速度は次第に速くなります。位置�Cに来た時、遠心力=万有引力となりますが、位置�Bから位置�Cに飛び出した勢いで、更に惑星は太陽から遠ざかります。そして、赤の領域に入ります。赤の領域では、万有引力＞遠心力なので、惑星の太陽から遠ざかる動きは次第に遅くなります。そして、位置�@に来た時、惑星の太陽から遠ざかる動きは止まります。そして、また同じことをくり返します。この様にして、惑星は太陽を１つの焦点とした楕円軌道を描きながら永遠に公転します。

�X.本当にその軌道は楕円か

　では、この惑星の公転軌道が本当に楕円なのかを検証します。

�@遠心力F= α/r³
�A万有引力F’= α/r²
でした。そして
�C遠心力Fと万有引力F’の差=α{(1/r³)−(1/r²)}
でした。

　ところで、惑星が同じ距離Lだけ公転するのに要する時間はβr[秒]です。公転速度vは軌道半径rに反比例するからです。
　また、力=質量m×加速度であり質量m=1とすると加速度=α(1/r³-1/r²)となります。そして距離=(1/2)×加速度×時間の2乗です。ですから太陽の重力による位置エネルギーを考慮しなければ
�D同じ距離L公転した時の惑星の落下又は飛び出す移動距離=(1/2)α(1/r³-1/r²)*β²*r²=(1/2)α*β²(1/r-1)
です。

　ただし、太陽の周りにはその重力による位置エネルギーがあります。
�E位置エネルギーU=−GMm/r　(GMmrの定義は前と同じ)
　この様に、位置エネルギーUは太陽からの距離rに反比例します。つまり、太陽から遠ざかる方向へ惑星に同じ力を加えても、遠ざかる距離は太陽からの距離rに比例します。

　例えば、太陽からの距離が2倍になれば、位置エネルギーUは1/2倍となるので惑星は動かし易くなり、遠ざかる距離も2倍となります。
　逆に、太陽に近づく方向へ同じ移動エネルギーを持つだけ惑星を動かすには、rに比例する距離だけ動かしてやらなければなりません。

　ですから、�Dと�Eより
�F同じ距離L公転した時の惑星の落下又は飛び出す移動距離=(1/2)α(1/r³-1/r²)*β²*r²*r=(1/2)α*β²(1−r)[m]
です。

　つまり、惑星はLだけ公転すると(1/2)α*β²(1−r)[m]太陽に近づくか遠ざかるのです。では、この公転軌道の形は何でしょうか。

�Y.惑星は楕円軌道を公転する

　惑星の公転軌道を検証します。
　楕円上に惑星qと楕円の中心Oとの反対側に惑星pがあります。この2つの位置の惑星が、左に同じ距離Lだけ回ります(時計と反対回り)。その位置をq’とp’とします。q’がこの楕円上にあれば、惑星は楕円軌道を公転し続けることになります。
　惑星がLだけ公転した時、太陽に近づき又は遠ざかる距離は�F(1/2)α*β²(1−r) でした。ですから距離L公転した時の
�Gr1の縮む長さ=(1/2)α*β² (1−r1)
�Hr2の伸びる長さ=(1/2)α*β² (1−r2)
です。
図は楕円なので、線分(S−q)+ 線分(S−p)= 線分(S−q)+ 線分(S’−q)= r1+r2=2です。∴�Ir2=2−r1です。�G�H�Iより
r1の縮む長さ+ r2の伸びる長さ=(1/2)α*β² (1−r1)+ (1/2)α*β² (1−r2)= (1/2)α*β² (2−r1−r2)= (1/2)α*β²{2−r1−(2−r1)}=(1/2)α*β²×0=0
です。
　つまり、Sq S’を結んだ長さとSq’ S’を結んだ長さは等しいのです。2つの焦点と円周上の任意の1点を結んだ長さが同じ図形は楕円です。ですからq’は楕円上にあります。
　この仕組みにより、惑星は永遠に楕円軌道上を公転します。証明終わり。

　※この証明方法を、「惑星楕円軌道のkothimaro解法」と呼びます(2016/11/03pm21:00)。

�Z.補足

　ここでは「完全な円軌道」を想定しています。
　そして、r>1の位置で惑星が円軌道を公転すると
遠心力F=α/(1.1)³<万有引力F’=α/(1.1)²
となるので、その力の差α(1/r³-1/ r²)だけ、惑星には太陽方向へ引かれる力が働き�@落下します。
　また、r<1の位置で惑星が円軌道を公転すると
遠心力F=α/(0.9)³>万有引力F’=α/(0.9)²
となるので、その力の差α(1/r³-1/ r²)だけ、惑星には太陽とは逆方向へ力が働き�A飛び出します。(1.1と0.9は、遠心力と万有引力の関係を説明するための便宜上の値です)

　つまり、幾ら惑星が円軌道を回ろうとしても、r>1の位置では太陽方向へ引かれ、r<1の位置では太陽とは逆方向へ飛び出す力に押され「円軌道から外れ続ける」と言う意味です。そして、この円軌道からの落下及び飛び出しを少しずつ続けながら惑星は公転します。

　惑星は、本来円軌道を取ろうとするのですが、その位置と公転速度では遠心力と万有引力とに差が生じ、その差力により本来惑星が取ろうとした円軌道よりズレた楕円軌道を公転するのです。

　一方、力学的エネルギー保存則は
�@(1/2)mv²−GMm/r=b=一定
です。b≧0だと、惑星は飛んで行ってしまうのでb<0です。また、角運動量保存則は
�Amvr=a=一定
です。
　では、この2つの法則を適用してこの惑星の公転軌道を求めます。
�Aより、�Bv=a/mr、�@と�Bより
(1/2)m(a/mr)²−GMm/r=(1/2)(a²/mr²)−GMm/r=b、b+ GMm/r−(a²/2mr²)=0、br²+GMmr−(a²/2m)=0 ∴r=[−GMm±√{(GMm)²+2ba²/m}]/2b、r>0なので、r=[−GMm−√{(GMm)²+2ba²/m}]/2b
です。
v= a/mr=(a/m)×1/r=(a/m)×2b/{−GMm−√((GMm)²+2ba²/m)}=2ab/m{−GMm−√((GMm)²+2ba²/m)}

　したがって、この惑星は半径r=[−GMm−√{(GMm)²+2ba²/m}/2b]メートルの円周上を速度v=2ab/m{−GMm−√((GMm)²+2ba²/m)}[m/s]で公転します。GMmabは与えられた値です。ですから半径rと速度vは変化しません。故に、本来惑星は「完全な円」を描きながら公転します。

　しかし前述のとおり、宇宙空間に漂う微小な塵の影響で惑星の公転速度が落ちると、遠心力が弱まり太陽に向かって落下します。太陽に近づくと今度は遠心力が強くなり惑星は太陽から遠ざかります。太陽から遠ざかると再び万有引力が強くなり惑星は太陽に向かって落下します。
　これを繰り返しながら、惑星は楕円軌道を公転します。

巨智麿研究室へ according to kothimaro