ガウスの相関予想(GCC)とは、「尾平均値が０の任意のn次元ガウス測度μとn次元ユークリッド空間の任意の対称な凸部分集合A、Bに対して、μ(A∩B)≧μ(A)×μ(B)が、成り立つ」と言う予想です。
この予想を簡単に表現するために、ダーツを例にします。
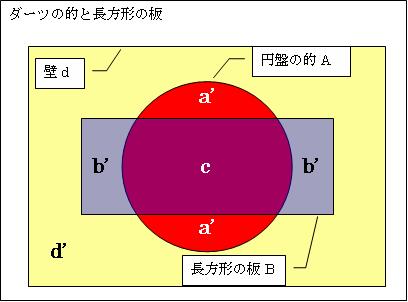左図のように、長方形の板の上にダーツの円盤を置きます。すると、ガウスの相関予想(GCC)は次のように翻訳されます。①「的にむかってダーツを投げた時、円板と長方形の板との重なった部分に刺さる確率は、円板だけに刺さる確率と長方形の板だけに刺さる確率の積以上になる」
説明を簡単にするために、次のように設定します。
円盤をA・板をB・壁をdとします。そして、ダーツは壁dの外には飛ばないとします。つまり、ダーツが壁dに刺さる確率を1とします。
円盤の的A(赤)の面積をa㎡、長方形の板B(青)の面積をb㎡、壁の面積をd㎡、円盤の的Aと長方形の板Bの重なった部分をc㎡、円盤Aからcを除いた部分をa'㎡、長方形の板Bからcを除いた部分をb'㎡、壁dの内円盤の的Aも長方形の板Bも無い部分をd'㎡とします。
ガウスの相関予想(GCC)は、「②2回ダーツを投げて赤い的Aと青い板Bに1回づつ当たる確率は、③1回ダーツを投げて赤い的Aと青い板Bの交わっている部分cに当たる確率以下である」とします。
しかし、これは本当に真でしょうか。
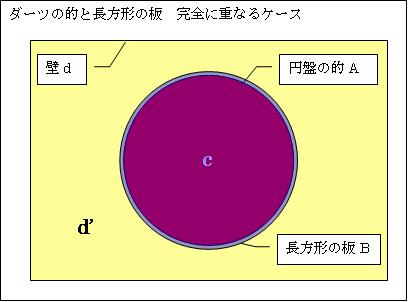赤い的Aと青い板Bが同じ形大きさで完全に重なるケースを想定します。これでは円盤も板も、重なる部分cのみとなります。すると、ガウスの相関予想(GCC)は「ダーツを2回投げて2回ともcに当たる確率は、1回投げてcに当たる確率以下である」となります。これは「真」です。
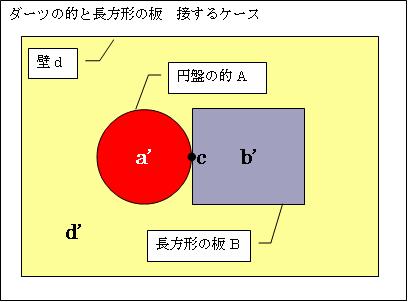次に、赤い的Aと青い板Bが接するケースを想定します。赤い的A全体が交わらない部分a'のみ、青い板全体が交わらない部分b'のみとなり、交わる部分cは点となりその面積は0㎡です。
すると、ガウスの相関予想(GCC)は「②ダーツを2回投げて赤い的Aと青い板Bに1回づつ当たる確率は、③１回ダーツを投げて点cに当たる確率以下である」となります。これは「偽」です。
なぜなら
赤い的Aに当たる確率=a'/d、青い板Bに当たる確率=b'/dなので、②= a'/d+ b'/d=(a'+b')/d>0です。一方、③=c/d=0/d=0です。∴②>③ですから。
こうして見ると、ガウスの相関予想(GCC)が成立するには、赤い的Aと青い板Bの交わり方が関係していることが分かります。
では、その成立要件を考察します。
②2回ダーツを投げて赤い的Aと青い板Bに1回づつ当たる確率=(a/d)(b/d)={(a'+c)/d}{(b'+c)/d}=c2/d2+(a'+b')c/d2+a'b'/d2
③1回ダーツを投げて赤い的Aと青い板Bの交わっている部分cに当たる確率=c/d
②=<③なので
c2/d2+(a'+b')c/d2+a'b'/d2< c/d
c/d>0なので、両辺をc/dで割ると
c/d+(a'+b')/d+a'b'/cd=④(a'+b'+c)/d+a'b'/cd =<1
です。
⑤(a'+b'+c)/dはダーツを1回投げて赤い的か青い板のどちらかに当たる確率です。そして、ダーツは壁dの何処かに必ず当たると仮定しているので、⑥赤い的と青い板どちらにも当たらない確率=d'に当たる確率=d'/dです。つまり
⑤+⑥=⑦(a'+b'+c)/d+d'/d=1
です。
④と⑦よりガウスの相関予想(GCC)が成立する要件は
⑧a'b'/cd=< d'/d
です。cd>0なので⑧の両辺にcdを掛けると
a'b'=< cd'
です。
d2>0なので、両辺をd2で割ると
(a'/d)(b'/d)=<(c/d)(d'/d)
です。
そして、a'/d=ダーツを1回投げてa'に当たる確率、b'/d=ダーツを1回投げてb'に当たる確率、c/d=ダーツを1回投げてcに当たる確率、d'/d=ダーツを1回投げてd'に当たる確率です。
ですから、ガウスの相関予想(GCC)が成立する要件は「ダーツを2回投げてそれぞれ赤い的と青い板の交わっていない部分a'とb'に当たる確率が、ダーツを2回投げてそれぞれ交わっている部分cと的も板も無い部分d'に当たる確率以下であること」となります。
的と板のある壁がどんどん遠ざかると、a'とb'とcに当たる確率は無限小に近づきます。それに比べて何もないd'はどんどん広くなり、d'に当たる確率は1に近づきます。ですから、壁が無限に遠いケースでは
(a'/d)(b'/d) =∞小×∞小=<(c/d)(d'/d)=∞小×1
となり、ガウスの相関予想(GCC)は常に成立するようになります。
