一方、鏡を使って光を往復させ、その速度を計測することは可能です。光は、私のいる場所から出発し、また私にいる場所に戻って来るからです。同一場所で同じ時計を使うので、私は、光が発した時と戻って来た時を正確に知ることが出来ます。これで、光の往復に要した時間を計ることが出来ます。
しかし、直線で光の速度を測ることが出来るでしょうか。
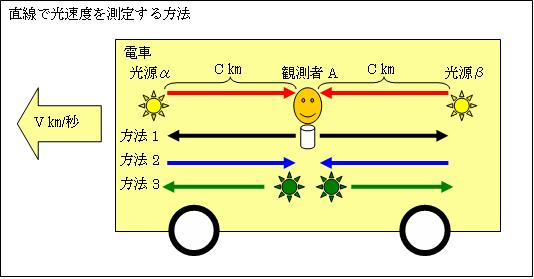今、v[m/s]で移動する電車の中で、観測者Aが光の速度を測定しています。便宜上、静止時には光源αβと観測者Aは、c[m]離れているとします。静止時には、光源αから来る光もβから来る光も、1秒で観測者Aに届きます。では、この電車がv[m/s]で移動した場合、光源αとβから光が発射された時を、観測者Aはどの様にして知ることが出来るでしょうか。
その方法は3つ考えられます。方法1は、白いスイッチを押し、「光を発せよ」と言う黒い矢印のシグナルを光源装置αとβに伝え、光を発射させる方法です。方法2は、光源αとβから、今「光が発射された」と言う青い矢印のシグナルを受け取る方法です。方法3は観測者Aの位置でAの持っている時計と時間を合わせ、緑の矢印の通りαとβの位置までその2つの時計を移動させ、光を発射した時を知るものです。
しかし、これらの方法で、光源αとβが光を発した時を知ることが出来るでしょうか。瞬時に伝わるものがあれば、発射時を知ることが出来ます。方法1では、スイッチを押すと光源αとβに瞬時に「光を発せよ」と言うシグナルが送られるので、光を発した時はシグナルを送った今です。方法2でも、αとβから「光を発した」と言うシグナルが瞬時に観測者Aに届くので、光を発した時はシグナルが届いた今です。
方法3では、時計を移動させると時計の進み方が変化してしまいます。これでは、観測者Aの持っている時計とαβの地点に移動させた時計が合っている保証はありません。
因果関係が伝わる速度は光速が最高です。では光速を使って、方法1と2で光速度が幾らと測定されるか検証して見ましょう。
先ず、方法1です。Aがスイッチを押して、αとβに光を発せよとの黒の矢印のシグナルが届くのは、何秒後でしょうか。「光速度を不変と仮定する」と、それは1秒後です。そして、観測者Aの元には2秒後に、αとβから光が届きます。αからもβからも、光を発して1秒後にその光が届きました。従って、光速度はc[m/s]と計算されます。
しかし、これでは、光を往復させて速度を測ったのと同じです。「Kothimaro変換」の説明の通り、往復させて測ると光は往復2c[m]を2秒で進むので、スイッチを押してから2秒後にαとβから光が届きます。
では、方法2ではどうでしょうか。「光速度を不変と仮定する」と、αとβから「光を発した」と言うシグナルは、実際に発射されてから1秒後にAの元に届きます。従って、αとβから光が発射されたのは1秒前です。従って、光の速度はc[m]÷1秒=c[m/s]と計算されます。
このことから分かる様に、直線で光速度を測ることは、「光速度を不変」と仮定すると、「光速度は不変」と計算されると言う循環論法なのです。
瞬時に伝わるものがないので、αとβから光が発射された時は観測者Aには分かりません。「光速度を不変」と仮定すると、Aの元に光が同時に届いたので、αとβは同時に光を発したと考えられます。「光速度は不変ではない」とすると、αとβが光を発した時は異なります。これが「同時性の相対性」です。
この様に、異なる地点で時を計ることが出来ないのです。光速度を直線で測るには、必然的に異なる地点で時を計ることになるので、不可能なのです。これに比べて、光を往復させて測る方法では、光の出発地点と到達地点が同一場所なので、光が発してから戻って来るのに要した時間を計ることが可能なのです。
では、往復させて光速度を測定して見ましょう。便宜上、装置の片道をc[m]とします。静止時には、全ての光は2秒で戻って来ます。私と装置がv[m/s]で移動するとどうでしょう。光の往復距離は縦(上下左右)は2c/√(1−v2/c2)[m]・横(進行方向)2c/(1−v2/c2)[m]となります。しかし、装置自体がローレンツ収縮し、横に√(1−v2/c2)倍となります。従って、光の往復距離は、縦横共に2c/√(1−v2/c2)[m]です。光の絶対速度はc[m/s]なので、光は縦も横も2/√(1−v2/c2)秒で往復します。
一方、v[m/s]で移動する時計は、質量が1/√(1−v2/c2)倍に増えた様に振る舞います。従って、静止時の√(1−v2/c2)倍しか動きません。つまり、この時計は、2/√(1−v2/c2)秒間に2秒を刻む様になります。
従って、v慣性系で光は、2c[m]÷2秒=c[m/s]とその速度は不変と計れるのです。
