光速度不変の原理とCATBIRD変換

　高速移動に伴う物質の質量増加・光速度の変化・物質の収縮による、時間と空間の主観的変化の仕組みを簡潔に解説する。

高速移動に伴う変化

　私が高速で移動すると、一体何が起こるだろうか。常識からすれば、他の物の移動速度が変化するだけである。時間の経過も空間の長さも、変わるとは思えない。しかしこれは、低速で移動した時の体験からそう思うのである。
　光速である299,792.5[�q/s](以後c[m/s]と表わす)が、あらゆるものの速度の限界と考えられている。この速度に近づくと、時間の経過が遅れ、空間は進行方向に伸びる。しかし、光の速度はcキロメートル/秒で変わらないと考えられている。つまり、光と対面する形で、高速で移動しながらその速度を測っても、光と並走する形でその速度を測っても、光は常にc[m/s]としか測れない。
　しかしこれは、常識に反するため大変理解しがたい。本ページでは、時間と空間とが変化する仕組みを述べる。そして、現実には光の速度は不変ではないことを証明する。それと同時に、光速度を不変と仮定して物理の計算をしなければならない理由も述べる。

　ローレンツ変換は、物質がvキロメートル/秒で移動すると、時間と空間は次の通り変化すると考える。一方、光の相対速度(移動する物質から見た速度)はcキロメートル/秒で不変である。t=時間、x=進行方向の距離、y=上下方向の距離、z=左右方向の距離、c=光の速度である。
t'= (t-(vx/c²)) / √（1-v²/c²）
x'=(x-vｔ)/√（1-v²/c²）
y'= y　
z'= z　
c'=c　
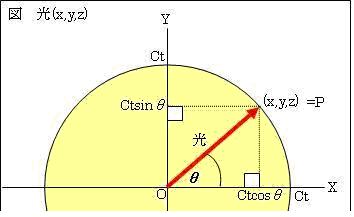　説明を簡単にする為に、平面で考える。光の座標をP(x,y,z)=(ctcosθ,ctsinθ,0)とする。ローレンツ変換式にx= ctcosθを代入すると、次の通り三角関数で表せる。
t'=t(c-vcosθ)/{c√(1-v²/c²)}
x'=(x-vｔ)/√（1-v²/c²）
y'= y
z'= z
c'=c

　しかし、vキロメートル/秒で移動するGPS衛星に内臓されている時計は1/ √（1-v²/c²）秒に1秒を刻む。この事実は、時間の変換式はt'=t/ √（1-v²/c²）であることを示している。
　変換後の光が進んだ距離は、√(x'²+y'²+z'²)= t(c-vcosθ)/√(1-v²/c²)である。これは光の速度と時間とでc't'とも表わせる。従って、c't'= t(c-vcosθ)/√(1-v²/c²)である。
　t'=t/ √（1-v²/c²）であるならば、c'=(c-vcosθ)でなくてはならない。つまり、地上で光は、(c-vcosθ)キロメートル/秒と観測されるはずである。

　それを示す実例を紹介する。ロケットの自動操縦に、リングレーザージャイロ装置が使われている。この装置では、光の相対速度を(c-vcosθ)キロメートル/秒と設定している。
　従って、正しい変換式は次の通りである。
t'=t/ √（1-v²/c²）
x'=(x-vｔ)/√（1-v²/c²）
y'= y
z'= z
c'=c-vcosθ (又はcosθ=x/ctを代入して) c'=(c-vx/ct)
　これをCATBIRD変換と名付ける(2012/8/17 PM17:19)。
　空間がこの様に変換された場合に、光行差を表わすブラッドリーの式sinβ=(v/c)sinαは成立する(注2を参照下さい)。 　従って、CATBIRD変換は、時間・空間・光速度の全てで、現実に観測される変化と一致している。

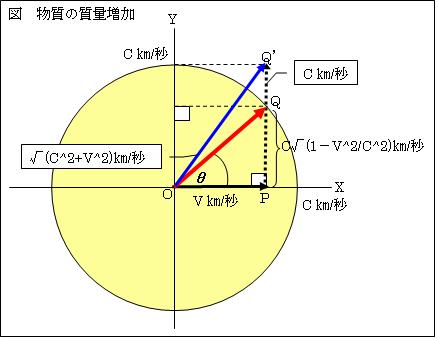
　CATBIRD変換する第一原因は、物質はvキロメートル/秒で移動すると、静止時に比べて√(1-v²/c²)しか動けなくなるからである。
　∠OPQ=90°とする。物質はvキロメートル/秒でOP進む。この物質を、Y軸方向にPからQ'までcキロメートル/秒で動かそうとしても出来ない。それでは物質の速度OQ'は、√(c²+v²)キロメートル/秒となり、光速を超えるからである。物質の速度OQはcキロメートル/秒が限界である。

　従って、PQは√(c²-v²)=c√(1-v²/c²)キロメートル/秒以上にはならない。速度は物質の質量に反比例する。よって、vキロメートル/秒で移動することにより物質は、質量が1/√(1-v²/c²)に増加した様に振舞う。

　物質は、それを構成する粒子が、結合したり離れたりすることで変化が進み時を刻む。従って、質量が増加すると粒子は動きにくくなり、結合と離れることに要する時間は1/√(1-v²/c²)倍となる。その為に、vキロメートル/秒で移動する物質は、ゆっくりと物質の反応が進み、1/√(1-v²/c²)秒に1秒を刻む。
　例えば、私が高速で移動すると、ゆっくりと動き思考し年を取る様になる。そして、私が静止している者を見ると、その者は速く動き思考し年を取っているのが見える。私には、あたかも静止者の時間は速く経過している様に見える。しかし、時間の経過自体は変化していない。変化したのは、私の物質としての反応速度の方である。これで、物質には速度に応じたそれぞれの時間の経過があることを上手に説明出来る。

　次に、空間の変化を述べる。v慣性系の1秒である1/√(1-v²/c²)秒間に、光は空間をc/√(1-v²/c²)キロメートル進む。従って、v慣性系に居る観測者は、c/√(1-v²/c²)キロメートルをcキロメートルと定義する。この結果、時間と空間及び光の速度は、次の通り変換される。
t'=t/√（1-v²/c²）
x'=x/√（1-v²/c²）
y'=y/√（1-v²/c²）
z'=z/√（1-v²/c²）
c'=c
　これを、第一変換と呼ぶ。

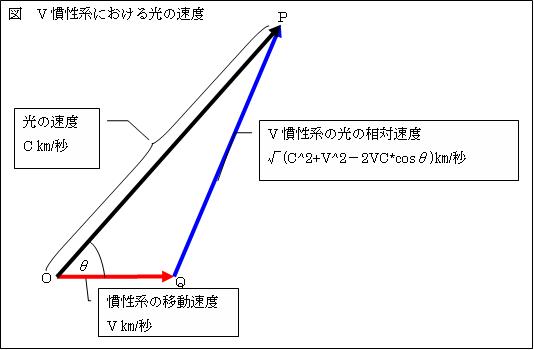
　次に、2つ目の原因を述べる。
　vキロメートル/秒で移動する慣性系では、光の速度は√(c²+v²-2cvcosθ)キロメートル/秒となる。これは第二余弦定理(PQ²=OP²+OQ²-2OPOQcosθ)より導くことが出来る。進行方向(横方向と言う)の空間は物質が移動した分、vtキロメートル変化している。上下左右方向(縦方向と言う)の空間に変化はない。時間の変化もない。従って、変換式は次の通りとなる。
t'=t
x'=x-vt
y'=y
z'=z
c'=√(c²+v²-2cvcosθ)
　これを、第二変換と呼ぶ。

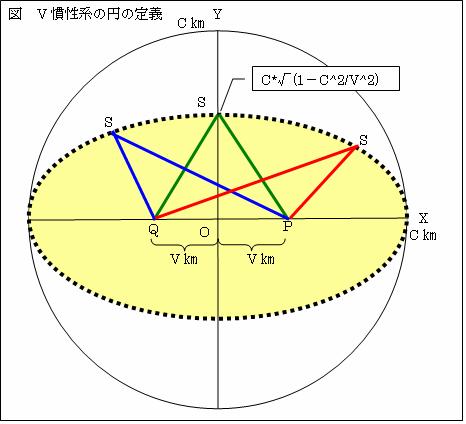
　では、物質がCATBIRD収縮した時、時間と空間はどう変わるかを述べる。
　半径cキロメートルの球体の鏡を想定する。この鏡は、平面で�@X²+Y²=c²と表わせる。静止時は、球体の中心Oから出発した光が、鏡に反射して再びOに戻るのに2秒かかる。そして、光の移動距離は2cキロメートルである。

　今度は、この鏡がvキロメートル/秒で移動する場面を考える。鏡の中心OはPからQに移動する。光の反射する位置をSとすると、光の通るルートはPSQとなる。球体の鏡がCATBIRD収縮すると、PSQ=2cキロメートルとなる。なぜなら、全ての方向において、光の往復距離は静止時と同じとなるからである。
　従って、点Sを結ぶと�AX²/c²+Y²/(c²-v²)=1の楕円となる。公式より、この楕円の2つの焦点PQと楕円上の任意の点Sとを結ぶ線の長さは、常に2cとなることから分かる。

　v慣性系では、あらゆる方向へ発した光が2秒で帰ってくる�AX²/c²+Y²/(c²-v²)=1の楕円を�@X²+Y²=c²の円と定義する。�Aの楕円は、�@の円を縦に√(1-v²/c²)収縮した形である。よって、v慣性系では空間が縦方向に√(1-v²/c²)収縮する。

　では、時間はどうなるであろうか。前述の通り、4つの力は2つの物質が光速で動くゲージ粒子を交換することで生じる。物質はCATBIRD収縮するので、4つの力が物質間を往復するのに要する時間は、静止時と同じである。従って、物質が変化するスピードは変わらず、時間は変化しない。光の速度√(c²+v²-2cvcosθ)は、空間が縦に√(1-v²/c²)収縮することにより、(c-vcosθ)キロメートル/秒と変換される(注1を参照下さい)。
　まとめると、変換式は次の通りとなる。
t'=t
x'=x
y'=y√(1-v²/c²)
z'=z√(1-v²/c²)
c'=(c-vcosθ)/√(c²+v²-2cvcosθ)
　これを第三変換と呼ぶ。

　第一・第二・第三変換を合わせると、次の通りCATBIRD変換となる。
t'=t/ √（1-v²/c²）
x'=(x-vｔ)/√（1-v²/c²）
y'= y
z'= z
c'=c-vcosθ

　以上の説明は、静止系が存在することを前提としている。特殊相対性理論では、光も物質も全て粒子であると考える。何もない空間を、粒子が動いていると説明する。すると、どの粒子が静止しているのか分からない。この粒子が静止していると考えると、あの粒子は移動している。逆にあの粒子が静止していると考えると、この粒子は移動しているとしか言えなくなる。全ての慣性系は、静止しているとも移動しているとも考えることの出来る平等なものとなる。
　この慣性系は静止しているいや移動していると考え方を変えただけで、光の速度が変化してはならない。従って、全ての慣性系で、光がcキロメートル/秒と観測されることが重要となる。　このために、特殊相対性理論は、光速度不変(c'=c)を前提として、ローレンツ変換を導いている。

　しかし、光も物質も超ひもの振動である。物質として振動している超ひもは物質に見える。振動していない超ひもは真空と見える。光も物質も、超ひもの上を波として伝わる。動かない超ひもの全体が静止系である。これで、静止系を基準として、それぞれの慣性系の移動速度を特定することが出来る。従って、光の速度は慣性系により異なっても良くなる。そうなると、自然にCATBIRD変換が導かれる。

　電磁力は、電磁波を交換し合う物質間の距離の2乗に反比例する。従って、移動する慣性系では、生じる電磁力の強さは、縦方向で(1-v²/c²)、横方向で(1-v²/c²)²に弱まると思える。
　しかし、電磁力の強さを求めるマックスウェルの方程式では、真空の誘電率と透磁率を定数としている。この2つは、電磁波の速度を決定する。従って、移動する慣性系でも、電磁波の速度は変わらない式となっている。この方程式で、移動する慣性系で生じる電磁力の強さ計算しても、静止時と変わらない。しかも、現実に移動する慣性系でも、生じる電磁力の強さは変わらないのである。ここから「光速度不変の原理」が導かれている。

　しかし、電磁波の相対速度が不変だから、生じる電磁力の強さが不変なのではない。物質がCATBIRD収縮する為に、電磁波の往復距離は常に静止時と同じとなるので、生じる電磁力の強さは不変なのである。

　ただ、一々電磁波の速度と物質間の距離の変化を計算して、生じる電磁力の強さを求めるのは無駄である。計算結果が同じなのであるから、電磁波の速度と物質間の距離を不変と仮定して、移動する慣性系でもマックスウェルの方程式を、そのまま使用する方が合理的である。これが「光速度不変の要請」である。

　観測者Aが、Oの位置で静止していれば、Pから届く光POは、c[m/s]と観測される。観測者Aが、OからQにv[m/s]で移動すると、光PQは、√(c²+v²-2vccosθ)[m/s]と観測される。これは、第二余弦定理より導くことが出来る。

　第一変換では、全ての方向において空間が1/ √（1-(v²/c²)倍となる。また、時間の経過も1/ √（1-(v²/c²)倍となる。速度=距離÷時間なので、光の速度は変化しない。

　第三変換では、縦方向のみ空間が√（1-(v²/c²)倍となる。つまり、PRがcsinθ[m/s]からcsinθ√(1-v²/c²)[m/s]となる。横方向の空間は変わらない。従って、OQ=v[m/s]、OR= ccosθ[m/s]、QR=(ccosθ-v)[m/s]である。また、時間の経過も変わらない。故に、観測される光の速度は変化する。



　では、第三変換後の光PQの速度を求める。
　変換後のPQ=√(QR²+変換後のPR²)
=√{(ccosθ-v)²+{csinθ√（1-v²/c²)}²}
=√（1-v²/c²)√{{(ccosθ-v)/√（1-v²/c²)}²+(csinθ)²}
=√（1-v²/c²)c√{(c²cosθ²-2cvcosθ+v²)/(c²-v²)}+sinθ²}
=√（1-v²/c²)c√{(c²cosθ²-2cvcosθ+v²+c²sinθ²-v²sinθ²)/(c²-v²)}
={√（1-v²/c²)/√{（1-v²/c²)}√{c²(cosθ²+sinθ²)-2cvcosθ+v²-v²(1-cosθ²)}
=√(c²-2cvcosθ+v²cosθ²)
=√(c-vcosθ)²=(c-vcosθ)[m/s]
となる。
　従って、縦方向に空間が√(1-v²/c²)倍となると、観測される光の速度は、√(c²+v²-2cvcosθ)[m/s]から（c-vcosθ)[m/s]に変化する。

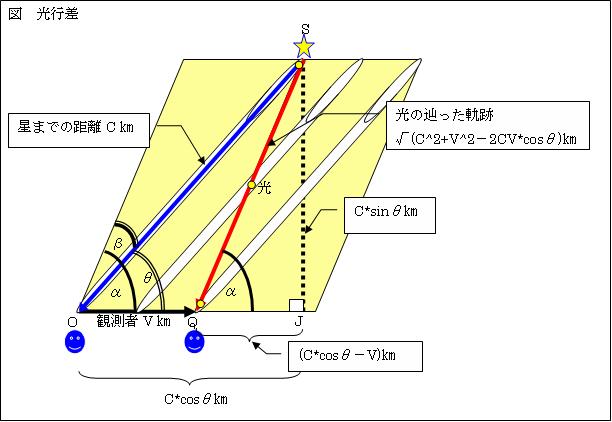
　星を望遠鏡で見る場合、実際に星のある方向に望遠鏡を向けても、その星は見えない。少し、地球の進行方向に望遠鏡を傾けてやらないと、その星は見えない。

　青線OSを観測者Aと星Sとの距離とする。観測者Aと望遠鏡は、速度v[m/s]でOからQへ移動する。観測者Aに届いた星Sからの光を、赤の矢印SQとする。
　望遠鏡を、実際に星がある方向に向けて∠α傾けたのでは、星Sからの光は望遠鏡を通り抜けることは出来ない。望遠鏡を∠θ傾けると、星Sからの光は、上手に望遠鏡を通り抜けて、Qの位置で観測者Aに届く。この∠αと∠θの差である∠βを光行差と言う。これは、ブラッドリーの式、sinβ=(v/c)sinαで表される。

　各区間の距離は、図の通りである。観測者Aと星Sとの距離OS=c[m]、観測者Aの移動距離OQ=v[m]、観測される光の速度SQ=√（c²＋v²-2cvcosθ）[m]である。また、星SからOQの延長線上に下ろした垂線の足をJとする。SJ= csinθ[m]、OJ= ccosθ[m]、QJ=(ccosθ-v)[m]である。

　この距離設定で、光行差∠βを求める。
sinα= csinθ/√(c²+v²-2vccosθ)
sinβ= sin(α-θ)= sinαcosθ-cosαsinθ　(公式より)
= (csinθ/√(c²+v²-2vccosθ)) cosθ-((ccosθ-v)/ √(c²+v²-2vccosθ)) sinθ
= (sinθ/√(c²+v²-2vccosθ))(c cosθ-ccosθ+v)= v sinθ/ √(c²+v²-2vccosθ)
∴sinβ=(v/c)sinα
となる。

　第一変換では、全ての方向の空間が、1/ √（1-(v²/c²)倍となるので、角度は変化しない。第三変換では、縦方向のみ空間が√(1-v²/c²)倍となる。従って、注1の通り、SJ= csinθ√(1-v²/c²)[m]、SQ=(c-vcosθ)[m]となる。しかし、距離の表記が変わるだけで、空間の実際の長さが変わる訳ではないので、角度は変わらない。従って、第三変換後においても、sinβ=(v/c)sinαが成立する。

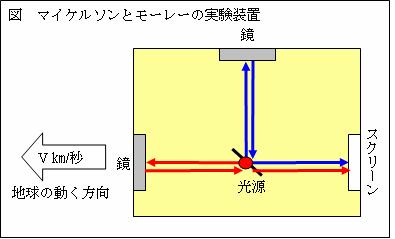
　マイケルソンとモーレーは、鏡を使い2本の光を、地球の進行方向(以後横方向と言う)と上下左右方向(以後縦方向と言う)に同じ距離往復させた。地球の速度をv[m/s]とする。すると、静止時に比べて、光の往復距離は、横方向では1/(1-v²/c²)倍、縦方向では1/√(1-v²/c²)倍に伸びる。従って、この2本の光は同時には戻らないはずである。しかし、その予想に反して、2本の光は同時に戻って来た。

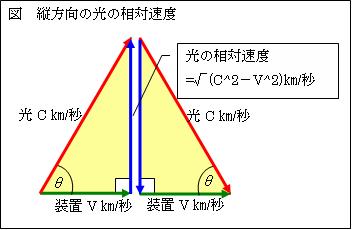　便宜上、この装置の片道をc[m]とする。縦方向には、往路も復路も、光の相対速度は√(c²-v²)[m/s]である。相対速度とは、移動する装置から見た光の速度を言う。これは、ピタゴラスの定理により求めることが出来る。従って、縦方向の往復に要する時間は、2c/√(c²-v²)秒である。
　では、光の絶対速度c[m/s]を使って、実際に光が往復する距離を求める。
　縦方向の往復距離=c[m/s]×2c/√(c²-v²)秒=2c²/√(c²-v²)[m]=2c/√(1-v²/c²)[m]
　静止時には、往復距離は2c[m]である。従って、往復距離は、1/√(1-v²/c²)倍となっている。

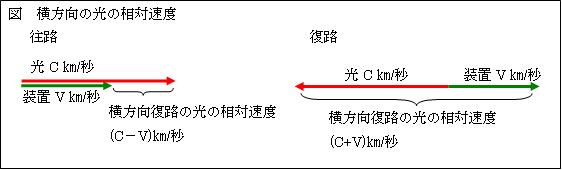　横方向の往路の光の相対速度は、(c-v)[m/s]である。従って、それに要する時間は、c/(c-v)秒である。横方向の復路の光の相対速度は(c+v)[m/s]である。従って、それに要する時間は、c/(c+v)秒である。横方向の往復に要する時間は、c/(c-v)+c/(c+v)=2c²/(c²-v²)秒である。

　では、光の絶対速度c[m/s]を使って、実際に光が往復する距離を求める。
　横方向の往復距離=c[m/s]×2c²/(c²-v²)秒=2c/(1-v²/c²)[m]
　静止時には、往復距離は2c[m]である。従って、往復距離は、1/(1-v²/c²)倍となっている。

　まとめると、v[m/s]で移動する慣性系では、光の往復距離は、縦方向では1/√(1-v²/c²)倍に、横方向では1/(1-v²/c²)倍となる。これでは、2本の光が同時に戻る事は出来ない。

　縦往復した光と、横往復した光が同時に戻るには、実験装置が縦方向へ√(1-v²/c²)倍に、横方向へ1/(1-v²/c²)倍に収縮しなければならない。その仕組みは、注4を参照下さい。これで
　縦方向の往復距離=2c√(1-v²/c²) /√(1-v²/c²)=2c[m]
　横方向の往復距離=2c(1-v²/c²) /(1-v²/c²)=2c[m]
　となり、2本の光は同時に戻ることが出来る。

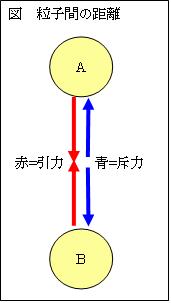
　物質を構成する粒子は、お互いに接し合っている訳ではない。粒子間には、電磁力等の引力と斥力とが働き、両者が釣り合う一定距離を保っている。
　電磁力は、電磁波が電荷を帯びた粒子間を往復することで生じる。電磁波は光でありc[m/s]で空間を伝わる。
　便宜上、粒子間の距離をc[m]と仮定する。v[m/s]で移動する慣性系では、注3の通り電磁波の往復距離は、縦方向には1/√(1-v²/c²)倍、横方向には1/(1-v²/c²)倍となる。しかし、粒子間に働く引力と斥力は、電磁波の往復距離が静止時と同じとなる距離で釣り合う。

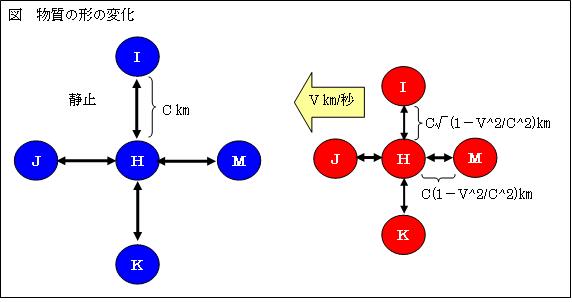
　従って、v[m/s]で移動する物質は、縦に√(1-v²/c²)倍、横に(1-v²/c²)倍収縮する。

TopPage 思考の迷宮へ according to CATBIRD