Top PageӮЦҒ@
ғҚҒ[ғҢғ“ғc•ПҠ·ӮөӮДӮаӢ——Ј=‘¬“xҒ~ҺһҠФӮЖӮИӮй
ҮT.ғҚҒ[ғҢғ“ғc•ПҠ·ӮЖӮН
Ғ@ғҚҒ[ғҢғ“ғc•ПҠ·ӮНҺҹӮМ’КӮиӮЕӮ·ҒB
Ү@x'=(x-vӮ”)/ҒгҒi1-v2/c2Ғj
ҮAy'= y
ҮBz'= z
ҮCt'= (t-vx/c2) / ҒгҒi1-v2/c2Ғj
ҮU.ғҚҒ[ғҢғ“ғc•ПҠ·ӮЕҒAҢхӮМҗiӮсӮҫӢ——ЈӮЖҺһҠФӮНӮЗӮӨ•ПҠ·ӮіӮкӮйӮ©
Ғ@ӮұӮМ•ы’цҺ®ӮНҒAv[m/s]ӮЕҲЪ“®ӮөӮҪҺһӮМҒAҺһҠФӮЖӢуҠФӮМ•ПҠ·Ӯр•\ӮөӮДӮўӮЬӮ·ҒB
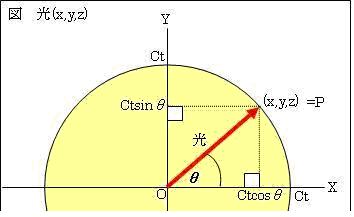 Ғ@җГҺ~ҢnӮЙӮЁӮҜӮйҢхӮМҚА•WӮр•ЦӢXҸг•Ҫ–КӮЕҒAP(x,y,z)=ҮD(ctcosғЖ,ctsinғЖ,0)ӮЖӮөӮЬӮ·ҒBҢхӮНҒAҢҙ“_OӮр”ӯӮөӮД1[s]ҢгӮЙPӮМҲК’uӮЙ“һ’BӮөӮЬӮ·ҒBҢхӮӘҲЪ“®ӮөӮҪҺһҠФӮНt[s]ӮЕӮ·ҒBҢхӮМҲЪ“®ӮөӮҪӢ——ЈӮНҒAҒг(x2,y2,z2)=Ғг{( ctcosғЖ)2+( ctsinғЖ)2+02}=ct[m]ӮЕӮ·ҒBҸ]ӮБӮДҒAҗГҺ~ҺТӮӘҢ©ӮҪҢхӮМ‘¬“xӮНҒAct[m]ҒҖt[s]=c[m/s]ӮЕӮ·ҒB
Ғ@җГҺ~ҢnӮЙӮЁӮҜӮйҢхӮМҚА•WӮр•ЦӢXҸг•Ҫ–КӮЕҒAP(x,y,z)=ҮD(ctcosғЖ,ctsinғЖ,0)ӮЖӮөӮЬӮ·ҒBҢхӮНҒAҢҙ“_OӮр”ӯӮөӮД1[s]ҢгӮЙPӮМҲК’uӮЙ“һ’BӮөӮЬӮ·ҒBҢхӮӘҲЪ“®ӮөӮҪҺһҠФӮНt[s]ӮЕӮ·ҒBҢхӮМҲЪ“®ӮөӮҪӢ——ЈӮНҒAҒг(x2,y2,z2)=Ғг{( ctcosғЖ)2+( ctsinғЖ)2+02}=ct[m]ӮЕӮ·ҒBҸ]ӮБӮДҒAҗГҺ~ҺТӮӘҢ©ӮҪҢхӮМ‘¬“xӮНҒAct[m]ҒҖt[s]=c[m/s]ӮЕӮ·ҒB
Ғ@ҚЎ“xӮНҒAv[m/s]ӮЕҲЪ“®Ӯ·ӮйҠП‘ӘҺТAӮӘ“ҜӮ¶ҢхӮрҢ©ӮйӮЖҒAӮ»ӮМ‘¬“xӮНҠфӮзӮЖҠП‘ӘӮіӮкӮйӮЕӮөӮеӮӨӮ©ҒBғҚҒ[ғҢғ“ғc•ПҠ·ӮЙӮжӮйӮЖҒAҢхӮМҗiӮсӮҫҺһҠФt[s]ӮНҒAvҠөҗ«ҢnӮЕӮНҮCӮМ’КӮи•ПҠ·ӮіӮкӮЬӮ·ҒBҮDӮжӮиҮEx=ctcosғЖӮЕӮ·ҒBҸ]ӮБӮДҒAҮEӮрҮCӮЙ‘г“ьӮ·ӮйӮЖ
vҠөҗ«ҢnӮЕҢхӮМҗiӮсӮҫҺһҠФҮCt'= (t-vx/c2) / ҒгҒi1-v2/c2Ғj=(c-vcosғЖ)t/cҒг(1-v2/c2)[s]
ӮЙ•ПҠ·ӮіӮкӮЬӮ·ҒB
Ғ@ӮЬӮҪҒAҢхӮМҗiӮсӮҫӢ——ЈҒг(x2,y2,z2)ӮНҒAvҠөҗ«ҢnӮЕӮНҮFҒг(x'2+y'2+z'2)ӮЙ•ПҠ·ӮіӮкӮЬӮ·ҒBӮұӮкӮЙҮDӮр‘г“ьӮ·ӮйӮЖҒA
vҠөҗ«ҢnӮЕҢхӮМҗiӮсӮҫӢ——ЈҮFҒг(x'2+y'2+z'2)=Ғг{((t-vx/c2) / ҒгҒi1-v2/c2Ғj)2+( ctsinғЖ)2+02}=(c-vcosғЖ)t/Ғг(1-v2/c2)[m]
ӮЙ•ПҠ·ӮіӮкӮЬӮ·ҒB
Ғ@Ҹ]ӮБӮДҒAv[m/s]ӮЕҲЪ“®Ӯ·ӮйҠП‘ӘҺТAӮ©ӮзҢ©ӮҪҢхӮМ‘¬“xӮНҒA(c-vcosғЖ)t/Ғг(1-v2/c2)[m]ҒҖ(c-vcosғЖ)t/cҒг(1-v2/c2)[s]=c[m/s]ӮЖӮИӮиӮЬӮ·ҒBӮұӮкӮЕҒAҠП‘ӘҺТӮМҲЪ“®‘¬“xvӮМ’lӮЙӮ©Ӯ©ӮнӮзӮёҒAҢх‘¬“xӮНҸнӮЙҗГҺ~ҢnӮЖ“ҜӮ¶c[m/s]ӮЖӮИӮиӮЬӮ·ҒBӮұӮкӮрҒuҢх‘¬“x•s•ПӮМҢҙ—қҒvӮЖҢҫӮўӮЬӮ·ҒB
Ғ@ӮұӮМ—lӮЙҒAғҚҒ[ғҢғ“ғc•ПҠ·ӮЕӮНҒAҺһҠФӮЖӢуҠФӮНҢх‘¬“xӮӘҸнӮЙc[m/s]ӮЙӮИӮй—lӮЙҳA“®ӮөӮД•ПҠ·ӮіӮкӮЬӮ·ҒB
ҮV.ғAғCғ“ғVғ…ғ^ғCғ“”ҺҺmҺ©җgӮЙӮжӮйүрҗа
Ғ@ӮұӮМ‘¬“x=Ӣ——ЈҒҖҺһҠФӮМҢvҺZӮр”Ы’иӮіӮкӮй•ыӮӘӢҸӮзӮкӮЬӮ·ҒBӮ»ӮМҲЧӮЙҒAғAғCғ“ғVғ…ғ^ғCғ“”ҺҺmӮӘғҚҒ[ғҢғ“ғc•ПҠ·ӮрӮЗӮМ—lӮЙҚlӮҰӮзӮкӮДӮўӮҪӮ©ӮрҢҹҸШӮөӮҪӮўӮЖҺvӮўӮЬӮ·ҒBҲИүәӮЕӮНҒAғAғCғ“ғVғ…ғ^ғCғ“”ҺҺmҺ©җgӮӘҸ‘Ӯ©ӮкӮҪҒw“БҺкӢyӮСҲк”К‘Ҡ‘Оҗ«—қҳ_ӮЙӮВӮўӮДҒxӮрҲш—pӮөӮЬӮ·ҒB
 Ғ„
Ғ„
x'=(x-vӮ”)/ҒгҒi1-v2/c2Ғj ҒEҒEҒEҒE(‘ж1Һ®)
y'= yҒEҒEҒEҒEҒEҒEҒEҒEҒEҒEҒEҒEҒEҒEҒEҒE(‘ж2Һ®)
z'= zҒEҒEҒEҒEҒEҒEҒEҒEҒEҒEҒEҒEҒEҒEҒEҒE(‘ж3Һ®)
t'= (t-vx/c2) / ҒгҒi1-v2/c2ҒjҒEҒE(‘ж4Һ®)
Ғ@ӮұӮкӮзӮМ•ы’цҺ®ҢQӮН<ғҚҒ[ғҢғ“ғc•ПҠ·>ӮЖҢДӮОӮкӮДӮўӮйҒB
Ғ@ғҚҒ[ғҢғ“ғc•ПҠ·ӮЙӮжӮкӮОҒAҗ^Ӣу’ҶӮМҢхӮМ“`”d–@‘ҘӮНҒAҠоҸҖ‘МKӮЙӮВӮўӮДӮаҠоҸҖ‘МK'ӮЙӮВӮўӮДӮа“ҜӮ¶ӮжӮӨӮЙ–һ‘«ӮіӮкӮйҒBӮұӮМӮұӮЖӮр’mӮйӮЙӮНҒAҺҹӮМ—бӮрҢ©ӮйӮЖҚD“sҚҮӮЕӮ ӮйҒBӮ ӮйҢхҗMҚҶ(җФӮМ–оҲу)ӮӘXҺІӮМҗі•ыҢьӮЙ‘—ӮзӮкӮДӮўӮйҒBӮұӮМҢхӮН•ы’цҺ®Ғu
x=ctҒv
ӮЙҸ]ӮБӮДҒA‘ҰӮҝ‘¬“xcӮЕ“`ӮнӮйҒBғҚҒ[ғҢғ“ғc•ПҠ·ӮМ‘ж1Һ®ӮЖ‘ж4Һ®ӮЙx=ctӮр‘г“ьӮ·ӮйӮЖ
x'=(c-v)t/Ғг(1-v2/c2)
t'=(1-v/c)t/Ғг(1-v2/c2)
ӮЖӮИӮйҒBx'ҒҖt'=cӮЙӮжӮБӮДҒA
Ғux'=ct'Ғv
ӮӘҸoӮДӮӯӮйҒBӮұӮМҺ®Ӯ©ӮзҒAҚА•WҢnK'ӮрҠоҸҖӮЖӮ·ӮйҺһӮМҢхӮМ“`”dӮӘ“ҫӮзӮкӮйҒBӮұӮМҺ®ӮжӮиҒAҠоҸҖ‘МK'Ӯ©ӮзҢ©ӮҪҢхӮМ‘Ҡ‘О“IӮИ“`”d‘¬“xӮаӮвӮНӮиcӮЕӮ ӮйӮұӮЖӮӘ•ӘӮ©ӮйҒB‘јӮМ”CҲУӮМ•ыҢьӮЙ“`”dӮ·ӮйҢхӮЙӮВӮўӮДӮа“Ҝ—lӮЕӮ ӮйҒB
ҒғҲИҸгӮЕӮ·ҒB
ҮW.’ҚҺЯ
Ғ@ӮұӮұӮ©ӮзӮНҒAҺ„ӮӘүрҗаӮөӮЬӮ·ҒBғAғCғ“ғVғ…ғ^ғCғ“”ҺҺmӮНҒA•ЦӢXҸгҒAҢхӮМҚА•WӮрP(x,y,z)=ҮG(ct,0,0)ӮЖ1ҺҹҢіӮЕ•\Ң»ӮіӮкӮДӮўӮЬӮ·ҒBҗГҺ~ҺТKӮ©ӮзҢ©ӮйӮЖҒAҢхӮНx=ctӮЕӮ·ҒBxӮНҢхӮМҗiӮсӮҫӢ——ЈӮЕӮ ӮиҒAtӮНҢхӮМҗiӮсӮҫҺһҠФӮЕӮ·ҒBҸ]ӮБӮДҒAKӮ©ӮзҢ©ӮйӮЖҢхӮМ‘¬“xӮНҒAx[m]ҒҖt[s]=ct[m]ҒҖt[s]=c[m/s]ӮЕӮ·ҒB
Ғ@ӮЕӮНҒAv[m/s]ӮЕҲЪ“®Ӯ·ӮйҠП‘ӘҺТK'Ӯ©ӮзҢ©ӮйӮЖҒAҢхӮМ‘¬“xӮНҠфӮзӮЙҢ©ӮҰӮйӮЕӮөӮеӮӨӮ©ҒBK'Ӯ©ӮзҢ©ӮҪҢхӮМҗiӮсӮҫӢ——ЈӮНҒAғҚҒ[ғҢғ“ғc•ПҠ·ӮМ‘ж1Һ®ӮЙx=ctӮр‘г“ьӮ·ӮйӮЖҒA
x'=(c-v)t/Ғг(1-v2/c2)[m]
ӮЕӮ ӮйӮұӮЖӮӘ•ӘӮ©ӮиӮЬӮ·ҒBӮЬӮҪҒAK'Ӯ©ӮзҢ©ӮҪҢхӮМҗiӮсӮҫҺһҠФӮНҒAғҚҒ[ғҢғ“ғc•ПҠ·ӮМ‘ж4Һ®ӮЙx=ctӮр‘г“ьӮ·ӮйӮЖҒAt'=(1-v/c)t/Ғг(1-v2/c2)[s]
ӮЕӮ ӮйӮұӮЖӮӘ•ӘӮ©ӮиӮЬӮ·ҒB
Ғ@Ҹ]ӮБӮДҒAK'Ӯ©ӮзҢ©ӮҪҢхӮМ‘¬“xӮНҒA
ҢхӮМҗiӮсӮҫӢ——ЈҒҖҢхӮМҗiӮсӮҫҺһҠФ=(c-v)t/Ғг(1-v2/c2)[m]ҒҖ(1-v/c)t/Ғг(1-v2/c2)[s]=c[m/s]
ӮИӮМӮЕҒAӮвӮНӮиҒAӮ»ӮМ‘¬“xӮНc[m/s]ӮЖ‘Ә’иӮіӮкӮЬӮ·ҒBӮұӮМӮұӮЖӮНҒAҢхӮӘXҺІӮМҗі•ыҢьӮЦҢьӮ©ӮӨҺһӮЙҢАӮзӮкӮёҒA‘SӮДӮМ•ыҢьӮЦҢьӮ©ӮӨҸкҚҮӮа“Ҝ—lӮЙҒAҢхӮНc[m/s]ӮЖ‘Ә’иӮіӮкӮЬӮ·ҒBӮұӮМ—lӮЙҒAғAғCғ“ғVғ…ғ^ғCғ“”ҺҺmӮНҸqӮЧӮзӮкӮДӮўӮЬӮ·ҒB
Ғ@2ҺҹҢіӮЕҚlӮҰӮҪҸкҚҮҒAҢхӮМҚА•WӮНҒAҸгӢLӮЕҺҰӮөӮҪ’КӮиP(x,y,z)=ҮD(ctcosғЖ,ctsinғЖ,0)ӮЕӮ·ҒBҺ„ӮНҒAҚЕҸүӮМҗа–ҫӮЕҒAғAғCғ“ғVғ…ғ^ғCғ“”ҺҺmӮӘ1ҺҹҢіӮЕҗа–ҫӮіӮкӮҪӮұӮЖӮр2ҺҹҢіӮЕҗа–ҫӮөӮҪӮҫӮҜӮЕӮ·ҒBҮGӮМ‘гӮнӮиӮЙҮDӮрҺgӮўҒA“Ҝ—lӮМҗа–ҫӮрҚsӮўӮЬӮөӮҪҒB
ҮX.Ӣ——Ј=‘¬“xҒ~ҺһҠФӮӘҗ¬—§Ӯ·Ӯй
Ғ@ғҚҒ[ғҢғ“ғc•ПҠ·ӮМ‘ж4Һ®ӮНҒAҗГҺ~ҢnӮМt[s]ӮНvҠөҗ«ҢnӮЕӮНt'[s]ӮЖӮИӮйӮұӮЖӮр•\Ң»ӮөӮДӮўӮЬӮ·ҒB‘ж1Һ®ҒE‘ж2Һ®ҒE‘ж3Һ®ӮНҒAҗГҺ~ҢnӮМx[m]ҒEy[m]ҒEz[m]ӮНvҠөҗ«ҢnӮЕӮНҒAx'[m]ҒEy'[m]ҒEz'[m]ӮЖӮИӮйӮұӮЖӮрҺҰӮөӮДӮўӮЬӮ·ҒBҸ]ӮБӮДҒAҗГҺ~ҢnӮЕҢ©ӮҪҢхӮМҗiӮсӮҫӢ——ЈҒг(x2,y2,z2)[m]ӮНҒAvҠөҗ«ҢnӮЕӮНҒг(x'2+y'2+z'2)[m]ӮЖӮИӮиӮЬӮ·ҒB
Ғ@‘¬“x=Ӣ——ЈҒҖҺһҠФӮЕӮ·ҒBҸ]ӮБӮДҒAv[m/s]ӮЕҲЪ“®Ӯ·ӮйҠП‘ӘҺТK'ӮӘҢхӮрҢ©ӮйӮЖҒAҢхӮМ‘Ҡ‘О‘¬“xӮНҒг(x'2+y'2+z'2)[m]ҒҖt'[s]=c[m/s]ӮЖӮИӮйӮЖҒAғAғCғ“ғVғ…ғ^ғCғ“”ҺҺmӮН–ҫүхӮЙҸqӮЧӮзӮкӮДӮўӮЬӮ·ҒB
Ғ@ҠП‘ӘҺТӮЖҢхҢ№ӮЖӮМ‘Ҡ‘О‘¬“xӮрv[m/s]ӮЖӮөӮЬӮ·ҒBӮ»ӮМҺһҒAӢуҠФӮЖҺһҠФӮМҚА•WӮНҒAҺҹӮМғҚҒ[ғҢғ“ғc•ПҠ·ӮМ’КӮи•ПҠ·ӮіӮкӮЬӮ·ҒB
Ү@x'=(x-vӮ”)/ҒгҒi1-v2/c2Ғj
ҮAy'= y
ҮBz'= z
ҮCt'= (t-vx/c2) / ҒгҒi1-v2/c2Ғj
үәҗ}ӮЙҠоӮГӮўӮДҗа–ҫӮөӮЬӮ·ҒB
 Ғ@ӮұӮМ•ы’цҺ®ӮНҒAv[m/s]ӮЕҲЪ“®ӮөӮҪҺһӮМҒAҺһҠФӮЖӢуҠФӮМ•ПҠ·Ӯр•\ӮөӮДӮўӮЬӮ·ҒB
Ғ@ӮұӮМ•ы’цҺ®ӮНҒAv[m/s]ӮЕҲЪ“®ӮөӮҪҺһӮМҒAҺһҠФӮЖӢуҠФӮМ•ПҠ·Ӯр•\ӮөӮДӮўӮЬӮ·ҒB
Ғ@җГҺ~ҢnӮЙӮЁӮҜӮйҢхӮМҚА•WӮр•ЦӢXҸг•Ҫ–КӮЕҒAP(x,y,z)=ҮD(ctcosғЖ,ctsinғЖ,0)ӮЖӮөӮЬӮ·ҒBҢхӮНҒAҢҙ“_OӮр”ӯӮөӮД1[s]ҢгӮЙPӮМҲК’uӮЙ“һ’BӮөӮЬӮ·ҒBҢхӮӘҲЪ“®ӮөӮҪҺһҠФӮНt[s]ӮЕӮ·ҒBҢхӮМҲЪ“®ӮөӮҪӢ——ЈӮНҒAҒг(x2,y2,z2)=Ғг{( ctcosғЖ)2+( ctsinғЖ)2+02}=ct[m]ӮЕӮ·ҒBҸ]ӮБӮДҒAҗГҺ~ҺТӮӘҢ©ӮҪҢхӮМ‘¬“xӮНҒAct[m]ҒҖt[s]=c[m/s]ӮЕӮ·ҒB
Ғ@ҚЎ“xӮНҒAv[m/s]ӮЕҲЪ“®Ӯ·ӮйҠП‘ӘҺТAӮӘ“ҜӮ¶ҢхӮрҢ©ӮйӮЖҒAӮ»ӮМ‘¬“xӮНҠфӮзӮЖҠП‘ӘӮіӮкӮйӮЕӮөӮеӮӨӮ©ҒBғҚҒ[ғҢғ“ғc•ПҠ·ӮЙӮжӮйӮЖҒAҢхӮМҗiӮсӮҫҺһҠФt[s]ӮНҒAvҠөҗ«ҢnӮЕӮНҮCӮМ’КӮи•ПҠ·ӮіӮкӮЬӮ·ҒBҮDӮжӮиҮEx=ctcosғЖӮЕӮ·ҒBҸ]ӮБӮДҒAҮEӮрҮCӮЙ‘г“ьӮ·ӮйӮЖ
vҠөҗ«ҢnӮЕҢхӮМҗiӮсӮҫҺһҠФҮCt'= (t-vx/c2) / ҒгҒi1-v2/c2Ғj=(c-vcosғЖ)t/cҒг(1-v2/c2)[s]
ӮЙ•ПҠ·ӮіӮкӮЬӮ·ҒB
Ғ@ӮЬӮҪҒAҢхӮМҗiӮсӮҫӢ——ЈҒг(x2,y2,z2)ӮНҒAvҠөҗ«ҢnӮЕӮНҮFҒг(x'2+y'2+z'2)ӮЙ•ПҠ·ӮіӮкӮЬӮ·ҒBӮұӮкӮЙҮDӮр‘г“ьӮ·ӮйӮЖҒA
vҠөҗ«ҢnӮЕҢхӮМҗiӮсӮҫӢ——ЈҮFҒг(x'2+y'2+z'2)=Ғг{((t-vx/c2) / ҒгҒi1-v2/c2Ғj)2+( ctsinғЖ)2+02}=(c-vcosғЖ)t/Ғг(1-v2/c2)[m]
ӮЙ•ПҠ·ӮіӮкӮЬӮ·ҒB
Ғ@Ҹ]ӮБӮДҒAv[m/s]ӮЕҲЪ“®Ӯ·ӮйҠП‘ӘҺТAӮ©ӮзҢ©ӮҪҢхӮМ‘¬“xӮНҒA(c-vcosғЖ)t/Ғг(1-v2/c2)[m]ҒҖ(c-vcosғЖ)t/cҒг(1-v2/c2)[s]=c[m/s]ӮЖӮИӮиӮЬӮ·ҒBӮұӮкӮЕҒAҠП‘ӘҺТӮМҲЪ“®‘¬“xvӮМ’lӮЙӮ©Ӯ©ӮнӮзӮёҒAҢх‘¬“xӮНҸнӮЙҗГҺ~ҢnӮЖ“ҜӮ¶c[m/s]ӮЖӮИӮиӮЬӮ·ҒBӮұӮкӮрҒuҢх‘¬“x•s•ПӮМҢҙ—қҒvӮЖҢҫӮўӮЬӮ·ҒB
Ғ@ӮұӮМ—lӮЙҒAғҚҒ[ғҢғ“ғc•ПҠ·ӮЕӮНҒAҺһҠФӮЖӢуҠФӮНҢх‘¬“xӮӘҸнӮЙc[m/s]ӮЙӮИӮй—lӮЙҳA“®ӮөӮД•ПҠ·ӮіӮкӮЬӮ·ҒB
ҢхӮМғhғbғvғүҒ[ҢшүК
Ғ@ӮұӮМ—lӮЙҒAҠП‘ӘҺТӮЖҢхҢ№ӮМ‘Ҡ‘О‘¬“xӮӘv[m/s]ӮЕӮ ӮйҺһҒAҢхӮМҗiӮсӮҫӢ——ЈӮНҗГҺ~ҺТӮӘҢ©ӮҪҸкҚҮct[m]ӮЕӮ·ӮӘҒAҠП‘ӘҺТӮӘҢ©ӮҪҸкҚҮҒAҮF=(c-vcosғЖ)t/Ғг(1-v2/c2)[m]ӮЖҠП‘ӘӮіӮкӮЬӮ·ҒB‘ҰӮҝҒAҢхӮМ”gӮМҺRӮ©ӮзҺRӮЬӮЕӮМӢ——Ј(”g’·)ӮНҒA(c-vcosғЖ)t/Ғг(1-v2/c2)[m]ҒҖct[m]=(1-vcosғЖ/c)/Ғг(1-v2/c2)”{ӮЖҠП‘ӘӮіӮкӮЬӮ·ҒB
Ғ@җU“®җ”Ғ~”g’·=Ңх‘¬ӮӘҗ¬—§ӮөӮЬӮ·ҒBҢх‘¬“xӮН•s•ПӮИӮМӮЕҒA”g’·ӮӘ(1-vcosғЖ/c)/Ғг(1-v2/c2)”{ӮЖӮИӮкӮОҒAҗU“®җ”ӮНҒг(1-v2/c2)/ (1-(v/c)cosғЖ)”{ӮЖӮИӮиӮЬӮ·ҒB‘ҰӮҝҒAҗU“®җ”ӮН
ғЛ'=ғЛҒ~Ғг(1-v2/c2)/ (1-(v/c)cosғЖ)
ӮЖӮИӮиӮЬӮ·ҒB

 Ғ@җГҺ~ҢnӮЙӮЁӮҜӮйҢхӮМҚА•WӮр•ЦӢXҸг•Ҫ–КӮЕҒAP(x,y,z)=ҮD(ctcosғЖ,ctsinғЖ,0)ӮЖӮөӮЬӮ·ҒBҢхӮНҒAҢҙ“_OӮр”ӯӮөӮД1[s]ҢгӮЙPӮМҲК’uӮЙ“һ’BӮөӮЬӮ·ҒBҢхӮӘҲЪ“®ӮөӮҪҺһҠФӮНt[s]ӮЕӮ·ҒBҢхӮМҲЪ“®ӮөӮҪӢ——ЈӮНҒAҒг(x2,y2,z2)=Ғг{( ctcosғЖ)2+( ctsinғЖ)2+02}=ct[m]ӮЕӮ·ҒBҸ]ӮБӮДҒAҗГҺ~ҺТӮӘҢ©ӮҪҢхӮМ‘¬“xӮНҒAct[m]ҒҖt[s]=c[m/s]ӮЕӮ·ҒB
Ғ@җГҺ~ҢnӮЙӮЁӮҜӮйҢхӮМҚА•WӮр•ЦӢXҸг•Ҫ–КӮЕҒAP(x,y,z)=ҮD(ctcosғЖ,ctsinғЖ,0)ӮЖӮөӮЬӮ·ҒBҢхӮНҒAҢҙ“_OӮр”ӯӮөӮД1[s]ҢгӮЙPӮМҲК’uӮЙ“һ’BӮөӮЬӮ·ҒBҢхӮӘҲЪ“®ӮөӮҪҺһҠФӮНt[s]ӮЕӮ·ҒBҢхӮМҲЪ“®ӮөӮҪӢ——ЈӮНҒAҒг(x2,y2,z2)=Ғг{( ctcosғЖ)2+( ctsinғЖ)2+02}=ct[m]ӮЕӮ·ҒBҸ]ӮБӮДҒAҗГҺ~ҺТӮӘҢ©ӮҪҢхӮМ‘¬“xӮНҒAct[m]ҒҖt[s]=c[m/s]ӮЕӮ·ҒB Ғ„
Ғ„ Ғ@ӮұӮМ•ы’цҺ®ӮНҒAv[m/s]ӮЕҲЪ“®ӮөӮҪҺһӮМҒAҺһҠФӮЖӢуҠФӮМ•ПҠ·Ӯр•\ӮөӮДӮўӮЬӮ·ҒB
Ғ@ӮұӮМ•ы’цҺ®ӮНҒAv[m/s]ӮЕҲЪ“®ӮөӮҪҺһӮМҒAҺһҠФӮЖӢуҠФӮМ•ПҠ·Ӯр•\ӮөӮДӮўӮЬӮ·ҒB