☆あらまし☆ 目次 トップページへ メールはこちら CATBIRDのブログ 発表論文
何故、移動系でもマックスウェルの方程式が使えるのか
移動系では、静止時に比べ電磁波の往復距離が伸びる。
生じる電磁力の強さは距離の2乗に反比例する為、移動系では電磁力が弱まると思える。
しかし、マックスウェルの方程式では、全ての系で生じる電磁力の強さは同じである。
☆目次☆
目次へ
1.慣性系が移動しても、電磁力現象は変わらないか
Ⅰ.電磁力に関する現象は、マックスウェルの方程式によって表現されます。
マックスウェルの方程式は
∇・B=0 E：電場 μ0：真空の透磁率
∂B/∂t+∇×E=0 B：磁場 j：電流
∇・E=P/ε0 P：電荷密度 ∇：ベクトル演算子
∂E/∂t-∇×B=μ0j ε0：真空の誘電率
です。生じる電磁力の強さは、ε0：真空の誘電率とε0：真空の透磁率
によります。この2つは、電磁波の伝わる速度を決定します。物質中と真空中とでは、電磁波の伝わる速度が異なり、
生じる電磁力の強さが異なります。
Ⅱ.移動系における電磁波の相対速度は、
√(c2+v2-2cvcosθ)[m/s] (第二余弦定理より)
と導けます。よって、物質中と真空中とにおける違いと同様に、静止系と移動系とでは、生じる電磁力の強さが異なると思えます。
Ⅲ.しかし、移動系においてもε0：真空の誘電率とε0：真空の誘磁率とを変えずに計算し、
その結果は現実に生じる電磁力の値に一致します。これでは、移動系においても、電磁波の速度は
√(c2+v2-2cvcosθ)[m/s]ではなく、c[m/s]と考えるしかない様に思えます。
これを、「光速度不変の原理」と言います。
目次へ
2.電磁力が働く仕組み
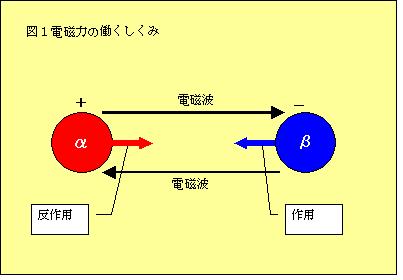Ⅰ.電磁力は、電荷を帯びた物質同士が、光である電磁波を交換し合うことにより働きます。
Ⅱ.図1では、便宜上、物質αを＋の電荷を帯びた物質、βを-の電荷を帯びた物質としています。
αとβは光である電磁波を交換し、βとα間には、引き寄せ合う作用・反作用が働きます。
Ⅲ.αから出発した電磁波はβに吸収され、今度はβから出発しαに届きます。そうして、
引き合う力が生じます。
Ⅳ.αとβが相対的位置関係を変えず、移動しながら電磁波を交換しあう場面を想定します。αβ間をL[m]とします。
電磁波の相対速度=√(c2+v2-2cv*cosθ)[m/s]
です。縦方向の往路と復路の電磁波の相対速度は、cosθ=v/cなので
√(c2-v2)[m/s]
となり、往復に要する時間は、
2L/√(c2-v2)秒
となり、その距離は、光の絶対速度はc[m/s]なので、
2Lc/√(c2-v2)=2L/√(1-v2/c2)[m]
となります。
Ⅵ.横方向の往路の電磁波の相対速度は、cosθ=1なので
(c-v)[m/s]
となり、往路に要する時間は、
L/(c-v)秒
となります。復路の電磁波の相対速度は、cosθ=-1なので
(c+v)[m/s]
となり、復路に要する時間は
L/(c+v)秒
となります。往復合計では
{L/(c-v)}+{L/(c+v)}=2Lc/(c2-v2)秒
となり、その距離は、電磁波の絶対速度はc[m/s]なので
2Lc2/(c2-v2)=2L/(1-v2/c2)[m]
となります。静止時における電磁波の往復距離は2L[m]でした。移動系では、この様に電磁波の往復距離は変わってきます。
Ⅴ.常識的に考えると、
電磁力は、αとβの距離の2乗に反比例するので、移動系では、上記の通り
電磁波の往復距離が静止時とは異なる為、αとβ間に生じる電磁力の強さは静止時とは異なった値となる様に思えます。
しかし、実際には静止系と移動系とでは生じる電磁力の強さは同じなのです。この矛盾の解法として、電磁波の相対速度は移動系においても変わらないとする「光速度不変の原理」
があります。電磁波の相対速度は√(c2+v2-2cvcosθ)[m/s]ではなく、c[m/s]と仮定します。
すると、移動系において電磁波がαβ間を往復するのに要する時間は、2L/c秒となり静止時と同じとなります。
これで、移動系においても、生じる電磁力の強さは静止時と同じであることを上手に説明出来ます。
しかし、ロケットの自動操縦に使うリングレーザージャイロ装置において、光の相対速度を(c-vcosθ)[m/s]と設定しており、
この宇宙において、光の相対速度は不変ではありません。
※光の相対速度√(c2+v2-2cvcosθ)[m/s]と(c-vcosθ)[m/s]の関係については、＞
v慣性系では光が、(c-vcosθ)[m/s]と観測される仕組み＜
を参照下さい。
目次へ
３．物質の縦横の収縮比率
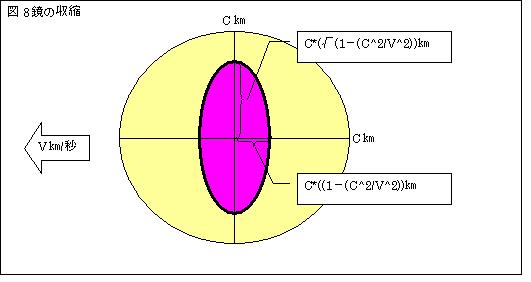
Ⅰ.上記の矛盾は、高速移動すると物質が収縮すると考えると解消されます。
電磁波を交換し合う物質間の距離L[m]を、左図では便宜上c[m]と設定しています。
静止時にはc[m]あった物質間の距離は、速度v[m/s]で移動すると、移動方向（X軸方向）へは、
(1-v2/c2)倍に収縮し、Y軸及びZ軸方向へは、
(√(1-v2/c2)倍に収縮します。
すると
縦方向の往復距離=2L*(√(1-v2/c2)/√(1-v2/c2)=2L[m]
横方向の往復距離=2L*(1-v2/c2)/(1-v2/c2)=2L[m]
となり、電磁波の往復距離は静止時と同一となり、生じる電磁力の強さは変わらないことを上手に説明出来ます。
目次へ
４．物質の大きさを決める要素
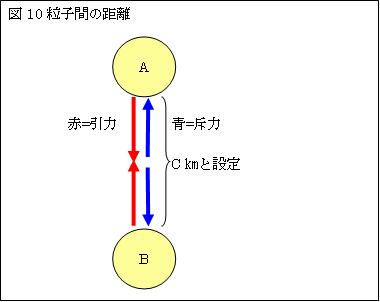
Ⅰ.物質を構成する粒子と粒子とは、お互いに接し合っているのではありません。一定距離を保っています。
何故、粒子同士は一定距離を保っているのでしょうか。
物質を構成する粒子と粒子間には、引力と斥力（反発力）とが双方働いています。引力と斥力は光速c[m/s]で伝わります。
Ⅱ.引力及び斥力は共に、粒子間の距離の2乗に反比例して強さが変化します。
距離L[m]で引力と斥力とは釣り合い、粒子はその距離を保ちます。その為に物質は一定の形をしています。
便宜上、左図では、L=c[m]と設定しています。
目次へ
５．物質が収縮する仕組み
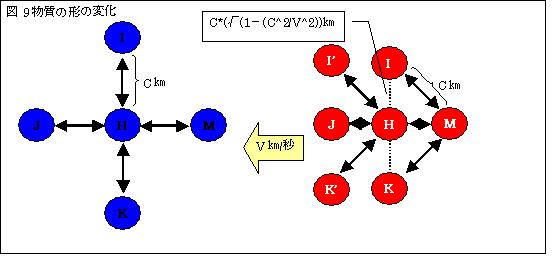
Ⅰ.青は、物質が静止している状態です。IとHは引力と斥力とが釣合い、一定距離を保っています。その距離を便宜上c[m]とします。
引力と斥力は1秒間で到達します。物質が速度v[m/s]で、左へ移動したとします。
速度vで移動する慣性系において、電磁波の相対速度は、
√（c2+v2-2cvcosθ）[m/s]
となります。IHは、進行方向とは90°の角度の位置にあるので、HからIへ（往路）はcosθ=v/cです。よって、電磁波の相対速度は
√（c2+v2-2v2）=√（c2-v2）[m/s]
です。IからHへ（復路）伝わる電磁波の速度も同値です。
従って、HI間がc[m]とすると、往路に要する時間は、
c/√（c2-v2)秒です。IH間の復路も同じ時間掛かります。往復2秒の位置で、
引力と斥力は釣り合うので、釣り合う距離は
2秒/(2c/√（c2-v2))秒=√(1-v2/c2)倍
に収縮します。
Ⅱ.進行方向間である、赤のJH間での引力・斥力の交換の場合は、HからJへの往路はcosθ=1、JからHへの復路はcosθ=-1です。
従って電磁波の伝わる速度は
HJ間(往路)=√（c2+v2-2cv）=(c-v)[m/s]
JH間（復路)=√（c2+v2+2cv）=(c+v)[m/s]
HJ間をc[m]とすると、往路に要する時間は、
c/(c-v)秒
復路に要する時間は、
c/(c+v)秒
合計で、
c/(c-v)+c/(c+v)=2c2/(c2-v2)秒
掛かります。往復2秒の位置で、引力と斥力は釣り合うので、釣り合う距離は
2/(2c2/(c2-v2))=(1-v2/c2)倍
となります。これをCATBIRD収縮と呼びます。
目次へ
６．物質の縦横の収縮差による電磁波の往復距離の不変性
Ⅰ.以上の仕組みにより、速度v[m/s]で移動する物質は、進行方向へ(1-v2/c2)、
上下左右方向へ√(1-v2/c2)の割合で収縮します。
速度vで移動する地球全体がこの様に収縮する為、地上における距離はこの通り収縮します。
従って、αから発した電磁波は、βに反射されαに戻りますが、その所要時間は
横方向={2/(1-v2/c2}*(1-v2/c2)=2秒
縦方向={2/(1-v2/c2)}*√(1-v2/c2)=2秒
と双方とも静止時と同値となります。電磁波の往復距離・所要時間とも不変です。
Ⅱ.速度vに関係なく、電磁波の軌跡は2cでなければなりません。
そうでないと、電磁波が往復するのに要する時間は変化し、生じる電磁力の強さも変わってきます。
ローレンツ収縮は、物質は横方向に√(1-v2/c2)収縮すると解しますが、これでは
縦方向の往復距離=2L/√(1-v2/c2)[m]
横方向の往復距離=2L*√(1-v2/c2)/(1-v2/c2)=2L/√(1-v2/c2)[m]
となり、速度vにより生じる電磁力の強さが変わってくる為、現実の宇宙にはマッチしません。
ただ、縦方向と横方向に往復した光は同時に戻って来れ、マイケルソンとモーレーの実験結果は説明可能ではあります。
しかし、CATBIRD収縮でMM実験の結果を説明すべきです。
目次へ
７．光速度不変の要請
Ⅰ.以上の様に、粒子同士がどの様に移動しながら電磁波を交換し合っても、
粒子間の距離の収縮率が方向により異なる為、その往復距離は静止時と同一です。静止時の粒子間の距離をc[m]と仮定すると、
速度vで物質が移動しても、電磁波の往復距離は全方向で2c[m]となり、粒子間に生じる電磁力の強さは、
常に静止時と同じであることが分ります。
Ⅱ.CATBIRD収縮により、マックスウェルの方程式で、物質が静止していても移動していても、その生じる電磁力の強さを正しく求めることが出来ます。
電磁力の相対速度が不変だから、物質の運動に関わらず、生じる電磁力の強さが一定なのではありません。
Ⅲ.しかし、一々電磁波の相対速度と粒子間の距離の変化を計算して、生じる電磁力の強さを求めることはことは大変煩雑です。
結果が同じであるなら、移動系でも電磁波の相対速度と粒子間の距離を不変と仮定した上で、
マックスウェルの方程式をそのままの形で使用し、電磁力の強さを計算する方が合理的です。この、
光速度を不変と仮定する思考方法が、「光速度不変の要請」ですｒ。
実際には、電磁波の相対速度は異なり、光速度不変はフィクションですが、不変と考えた方が物理計算上便利です。
目次へ
８.全ての物理現象への応用
Ⅰ.重力と強い力及び弱い力も全て、光速で動く粒子(=振動）を交換し合って、
作用・反作用が生じます。上記と同じ理由により、慣性系がどの様に移動していても、
静止時の物理法則に関する方程式がそのまま使えるのです。
Ⅱ.この仕組みにより、「どの様に移動する慣性系においても、
物理法則は形を変えない。」と言う要求は満たされるです。
