戞堦晹岝懍搙晄曄丂(暔棟丒悢妛丒惗暔丒楌巎丒揘妛丒廆嫵偺枹夝寛栤戣傪埖偄傑偡丅婱曽傕傾僀僨傾傪儕儕乕僗偟偰尒傑偟傚偆丅偄偞巚峫偺柪媨傊)
岝懍搙晄曄偺尨棟偺巇慻傒丂CATBIRD挊
嘥.崅懍堏摦偡傞偲丄帪娫偼抶傟嬻娫偼怢傃傞丅偟偐偟丄岝懍搙偼曄傢傜側偄丅
丂巹偑崅懍偱堏摦偡傞偲丄偳偺條側曄壔偑尰傟傞偱偟傚偆偐丅晛捠偵峫偊傟偽丄懠偺暔偺堏摦懍搙偑曄傢偭偰尒偊傞偱偟傚偆丅帪娫傗嬻娫偑曄壔偡傞偲偼巚偊傑偣傫丅帪娫傗嬻娫偼愨懳揑偱偡丅偦傟偵斾傋偰丄暔偺懍搙偼憡懳揑偱偡丅偟偐偟丄偙傟偼掅懍偱堏摦偟偨帪偺宱尡偐傜偦偺條偵巚偆偺偱偡丅
丂崅懍偱堏摦偡傞巹偺帪娫偲嬻娫偼曄壔偟傑偡丅偦偺帪丄巹偺帪娫偼備偭偔傝偲宱夁偟傑偡丅偦偟偰丄巹偺嬻娫偼怢傃傑偡丅偙偺條偵丄帪娫偲嬻娫偑堦懱偲偟偰曄壔偡傞偺偱丄娤應偝傟傞岝偺懍搙偼c[m/s]偱晄曄偲側傝傑偡丅偙偆尵偆堄枴偱丄岝懍搙偼愨懳揑偱偡丅偦傟偵斾傋偰丄帪娫偲嬻娫偼憡懳揑側偺偱偡丅
丂偟偐偟丄暲憱偟側偑傜岝偺懍搙傪應傞偲丄岝偺懍搙偼抶偔側傝偦偆偵巚偊傑偡丅傑偨丄懳柺偡傞宍偱岝偺懍搙傪應傞偲丄岝偺懍搙偼懍偔側傝偦偆偱偡丅偦傟偱傕憡懳惈棟榑偼丄憃曽偲傕岝偺懍搙偼c[m/s]偲偟偐應傟側偄偲偟傑偡丅偙傟傪丄乽岝懍搙晄曄偺尨棟乿偲尵偄傑偡丅
丂帪娫傗嬻娫偑曄壔偟丄傑偨岝偺憡懳懍搙(堏摦偡傞巹偐傜尒偨岝偺懍搙)偼曄傢傜側偄偲尵偆偺偼丄戝曄棟夝偟擄偄偙偲偱偡丅偦偺堊偵丄崱傑偱懡偔偺恖偺摢傪擸傑偣偰棃傑偟偨丅巹偼丄偙偺儂乕儉儁乕僕偱丄偦偺巇慻傒傪夝柧偟傛偆巚偄傑偡丅
嘦.v[m/s]偱堏摦偡傞帪寁偼丄1昩娫偵併(1-v2/c2)昩傪崗傓
丂愭偢丄岝懍偱堏摦偡傞偲丄帪娫偑抶偔側傞巇慻傒傪夝愢偟傑偡丅幚嵺偵丄崅懍偱堏摦偡傞帪寁偼抶傟傑偡丅崅懍偱堏摦偡傞GPS塹惎偵搵嵹偝傟偰偄傞帪寁偼抶傟傞偺偱丄彮偟懍偔恑傓條偵挷惍偝傟偰偄傑偡(偙偙偱偼丄廳椡偵傛傞帪寁偺抶傟偼峫偊傑偣傫)丅
丂GPS塹惎偺懍搙傪v[m/s]偲偟傑偡丅搵嵹偝傟傞帪寁偼丄抧忋偱偼1昩娫偵1/併(1-v2/c2)昩傪崗傓條偵愝掕偝傟偰偄傑偡丅GPS塹惎偑婳摴偵忔偭偨帪丄帪寁偑挷惍偝傟偰偄側偄偲丄1昩娫偵併(1-v2/c2)昩傪崗傓條偵側傝傑偡丅廬偭偰丄挷惍偝傟偨帪寁偼丄婳摴忋偱偼1昩娫偵1/併(1-v2/c2)昩亊併(1-v2/c2)=1昩傪崗傓條偵側傝丄抧忋偺帪寁偲僔儞僋儘偟傑偡丅
丂憡懳惈棟榑偱偼偙偺尰徾傪丄乽vkm/昩偱堏摦偡傞暔幙偼丄幙検偑1/併(1-v2/c2)攞偵憹壛偟偨條偵怳晳偆丅乿偲昞尰偟傑偡丅
 丂偟偐偟丄幚嵺偵幙検偑憹壛偡傞栿偱偼偁傝傑偣傫丅v[m/s]偱堏摦偡傞暔幙偼丄惷巭帪偵斾傋偰併(1-v2/c2)攞偟偐摦偗側偔側傞偺偱丄偙偺條偵昞尰偡傞偺偱偡丅
丂偟偐偟丄幚嵺偵幙検偑憹壛偡傞栿偱偼偁傝傑偣傫丅v[m/s]偱堏摦偡傞暔幙偼丄惷巭帪偵斾傋偰併(1-v2/c2)攞偟偐摦偗側偔側傞偺偱丄偙偺條偵昞尰偡傞偺偱偡丅
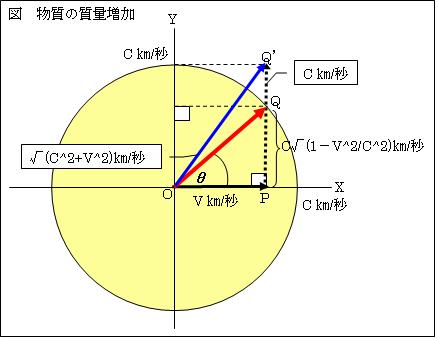
丂偱偼壗屘丄v[m/s]偱堏摦偡傞暔幙偼丄惷巭帪偺併(1-v2/c2)攞偟偐摦偗側偔側傞偺偱偟傚偆偐丅偦偺偙偲傪愢柧偟傑偡丅v[m/s]偱X幉曽岦傊堏摦偡傞棻巕兛偵丄堏摦僄僱儖僊乕傪壛偊偰Y幉曽岦傊摦偐偟傑偡丅棻巕兛偑惷巭偟偰偄傞帪偼丄Y幉曽岦傊嵟戝c[m/s]偱摦偐偡偙偲偑弌棃傑偡丅偟偐偟丄v[m/s]偱堏摦偡傞棻巕兛偼丄Y幉曽岦傊併(c2-v2)[m/s]偱偟偐摦偐偡偙偲偼弌棃傑偣傫丅
丂偙偺帪丄棻巕兛偺懍搙偼併[{併(c2-v2)}2+v2]=c[m/s]偲側傝傑偡丅棻巕兛偑丄Y幉曽岦傊併(c2-v2)[m/s]傪挻偊偰摦偔偲丄偦偺懍搙偼c[m/s]傪挻偊偰偟傑偄傑偡丅偁傜備傞傕偺偺懍搙偼c[m/s]偑尷奅偱偡丅偦偺堊偵丄偦傟埲忋偺懍偝偱Y幉曽岦傊摦偐偡偙偲偼弌棃側偄偺偱偡丅
丂惷巭帪偵偼丄棻巕兛傪c[m/s]偱摦偐偡偙偲偑弌棃傑偟偨丅v姷惈宯偱偼併(c2-v2)[m/s]偱偟偐摦偐偡偙偲偑弌棃側偔側傝傑偡丅廬偭偰丄棻巕偼丄v姷惈宯偱偼惷巭宯偵斾傋偰併(c2-v2)[m/s]亐c[m/s]=併(1-v2/c2)攞偺懍搙偱偟偐摦偗側偄偺偱偡丅
丂棻巕偺懍搙偑岝懍偵嬤偯偔掱丄壛懍偟擄偔側傞帠幚偼丄壛懍婍偺幚尡偱幚徹偝傟偰偄傑偡丅憡懳惈棟榑偼丄偦偺尰徾傪m=m0/併(1-v2/c2)偲昞偟傑偡丅m=v[m/s]偱摦偔暔幙偺幙検丄m0=惷巭帪偺暔幙偺幙検偱偡丅偦偟偰丄僇僂僼儅儞偼丄條乆側懍搙偺揹巕傪嬋偘傞幚尡傪峴偄丄憡懳惈棟榑偺捠傝偵揹巕偼摦偐偟擄偔側傞偙偲傪妋擣偟傑偟偨丅
丂偮傑傝丄vkm/昩偱堏摦偡傞帪寁偺撪晹偺峔憿偼丄惷巭帪偵斾傋偰丄併(1-v2/c2)攞偱偟偐摦偐側偔側傝傑偡丅廬偭偰丄偙偺帪寁偼1昩娫偵併(1-v2/c2)昩傪崗傓條偵側傝傑偡丅屘偵丄帪娫偺曄姺幃偼丄
嘆t'=t*併(1-v2/c2)
偲側傝傑偡丅t=1傪嘆偵戙擖偡傞偲丄t'=併(1-v2/c2)昩偲側傝傑偡丅偙傟偼丄惷巭宯偺1昩娫偵丄v姷惈宯偺帪寁偼併(1-v2/c2)昩傪崗傓偙偲傪昞偟偰偄傑偡丅
嘨.v姷惈宯偱偼丄嬻娫偼墶曽岦偵1/併(1-v2/c2)攞怢傃傞
丂偦偺帪丄嫍棧偼偳偺條偵應傟傞偱偟傚偆偐丅嫍棧傪應傞偵偼丄掕婯偱應傞曽朄偲丄岝傪摉偰偰應傞曽朄偲偑偁傝傑偡丅屻幰傪愢柧偟傑偡丅栚揑暔偵儗乕僓乕傪摉偰丄巹偺強偵斀幩偟偰曉偭偰棃傞傑偱偺帪娫傪寁傝傑偡丅岝偺墲暅偵梫偟偨帪娫亊岝懍c[m/s]亐2偱丄巹偐傜栚揑暔傑偱偺嫍棧傪寁嶼偟傑偡丅
偙偺2偮偺曽朄偱嫍棧傪應傞偲丄墶曽岦(恑峴曽岦)偱偼嫍棧偑1/併(1-v2/c2)攞挿偔應傟傞偺偱偡丅偙傟偵斾傋偰丄廲曽岦(忋壓嵍塃曽岦)偱偼曄壔偼偁傝傑偣傫丅
嘩.偦傟偼丄掕婯偑儘乕儗儞僣廂弅偡傞偐傜偱偁傞
丂掕婯偱應偭偨応崌丄墶曽岦偱偼挿偝偑1/併(1-v2/c2)攞偲應傟傞偙偲傪愢柧偡傞偵偼丄愭偢乽儘乕儗儞僣廂弅乿傪抦傜偹偽側傝傑偣傫丅
丂v[m/s]偱堏摦偡傞掕婯偼丄墶曽岦偵併(1-v2/c2)攞廂弅偟傑偡丅偙傟傪乽儘乕儗儞僣廂弅乿偲尵偄傑偡丅偦偺巇慻傒傪丄夝愢偟傑偡丅
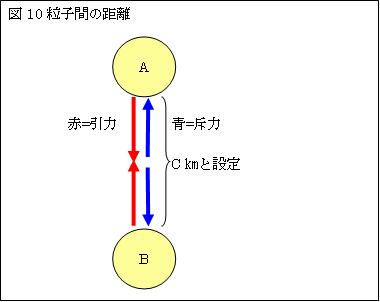 丂暔幙傪峔惉偡傞棻巕摨巑偼丄偍屳偄偵愙偟崌偭偰偄傞栿偱偼偁傝傑偣傫丅棻巕娫偵摥偔堷椡偲愃椡偲偑掁傝崌偆堦掕嫍棧傪曐偭偰偄傑偡丅暔幙偑崅懍偱堏摦偡傞偲丄偙偺堷椡偲愃椡偺僶儔儞僗偑曄壔偟丄暔幙偼墶曽岦偵併(1-v2/c2)攞廂弅偡傞偺偱偡丅
丂暔幙傪峔惉偡傞棻巕摨巑偼丄偍屳偄偵愙偟崌偭偰偄傞栿偱偼偁傝傑偣傫丅棻巕娫偵摥偔堷椡偲愃椡偲偑掁傝崌偆堦掕嫍棧傪曐偭偰偄傑偡丅暔幙偑崅懍偱堏摦偡傞偲丄偙偺堷椡偲愃椡偺僶儔儞僗偑曄壔偟丄暔幙偼墶曽岦偵併(1-v2/c2)攞廂弅偡傞偺偱偡丅
丂埲壓丄曋媂忋丄棻巕娫偺嫍棧傪c[m]偲偟偰愢柧偟傑偡丅
丂尨巕偼丄僾儔僗偺揹壸傪懷傃偨尨巕妀偲丄儅僀僫僗偺揹壸傪懷傃偨揹巕偲偐傜惉傝傑偡丅尨巕妀偺廃傝傪揹巕偑夞偭偰偄傑偡丅揹巕偼丄夞揮偵傛傝惗偠傞墦怱椡偲尨巕妀偵揹帴婥椡偱堷偒晅偗傜傟傞椡偲偑摍偟偔側傞嫍棧傪曐偪丄偦偺婳摴忋傪夞偭偰偄傑偡丅
丂偙傟偱偼丄尨巕偺廃傝偼儅僀僫僗偺揹壸傪懷傃偨揹巕偑暘晍偡傞偙偲偲側傝丄尨巕摨巑偼斀敪偟崌偆敜偱偡丅偱偼壗屘丄尨巕摨巑偼斀敪偟崌偄僶儔僶儔偲偼側傜偢丄偍屳偄偵寢崌偟偰寢徎傗暘巕傪宍惉偟偰偄傞偺偱偟傚偆偐丅
丂尨巕摨巑偼丄揹巕傪嫟桳偡傞偙偲偵傛傝寢崌偟偰偄傑偡丅偙傟傪嫟桳寢崌偲尵偄傑偡丅嫟桳偝傟偨揹巕偼丄暘巕婳摴傪夞傝傑偡丅暘巕婳摴傪夞傞揹巕偼丄尨巕妀偲尨巕妀偲偺娫偵丄揹巕枾搙偺崅偄椞堟傪宍惉偟傑偡丅偙偆偟偰丄僾儔僗偺揹壸傪懷傃偨2屄偺尨巕妀偺娫偵丄儅僀僫僗偺揹壸傪懷傃偨揹巕偑枾廤偡傞晹暘偑宍惉偝傟傞偺偱偡丅廬偭偰丄2屄偺僾儔僗偺揹壸傪懷傃偨尨巕妀偼丄偍屳偄偺娫偵偁傞儅僀僫僗偺揹壸傪懷傃偨揹巕偺崅枾搙晹暘偵堷偒晅偗傜傟傑偡丅
丂
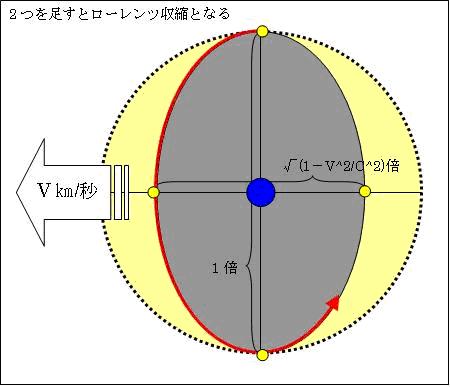 丂傑偨丄尨巕婳摴傪夞傞揹巕摨巑偼偍屳偄偵斀敪偟崌偄傑偡丅偙偺條偵偟偰丄尨巕摨巑偼丄偦偺娫偵堷椡丒愃椡丒墦怱椡偑摥偒丄偦偺椡偺僶儔儞僗偺庢傟偨嫍棧傪曐偪側偑傜丄嫮偔寢崌偟偰偄傞偺偱偡丅
丂傑偨丄尨巕婳摴傪夞傞揹巕摨巑偼偍屳偄偵斀敪偟崌偄傑偡丅偙偺條偵偟偰丄尨巕摨巑偼丄偦偺娫偵堷椡丒愃椡丒墦怱椡偑摥偒丄偦偺椡偺僶儔儞僗偺庢傟偨嫍棧傪曐偪側偑傜丄嫮偔寢崌偟偰偄傞偺偱偡丅
丂2屄偺尨巕偑v[m/s]偱堏摦偡傞偲丄偦偺椡偺僶儔儞僗偑曄壔偟尨巕娫偺嫍棧偑曄傢傝傑偡丅偦偟偰丄暔幙偼儘乕儗儞僣廂弅偟傑偡丅
丂墶曽岦偵併(1-v2/c2)攞廂弅偟偨掕婯傪巊偭偰丄嫍棧傪應偭偰傒傑偟傚偆丅嬻娫偺幚懱偼乽挻傂傕偺栐乿偱偡丅偙偺忋傪岝偼c[m/s]偱揱傢傝傑偡丅墶曽岦偼c[m]偺挿偝偺乽挻傂傕偺栐乿傪c/併(1-v2/c2)[m]偲應傝傑偡丅廲曽岦偱偼c[m]偺挿偝偺乽挻傂傕偺栐乿傪c[m]偲應傝傑偡丅廬偭偰丄嬻娫偺曄壔偼
嘇x'=x/併(1-v2/c2)
嘊y'=y
嘋z'=z
偲側傝傑偡丅
嘪.儗乕僓乕憰抲偲抶傟偨帪寁偱應偭偰傕丄墶曽岦偺嫍棧偼1/併(1-v2/c2)攞偲側傞
丂崱搙偼丄儗乕僓乕憰抲偲帪寁傪巊偭偰嫍棧傪應偭偰尒傑偡丅巹偲栚揑暔偲偺嫍棧傪c[m]偲偟傑偡丅惷巭帪偵偼丄廲曽岦傕墶曽岦傕丄栚揑暔偵斀幩偟偨儗乕僓乕偼2昩偱巹偺強偵栠偭偰棃傑偟偨丅岝偺愨懳懍搙偼c[m/s]偱偡丅廬偭偰丄墲暅嫍棧偼2昩亊c[m/s]=2c[m]偲寁嶼偝傟傑偡丅曅摴偺嫍棧偼2c[m]亐2=c[m]偱偡丅
丂師偼丄巹偲栚揑暔偲偼v[m/s]偱暲憱偟偰偄傑偡丅偙偺帪丄巹偲栚揑暔偲偺嫍棧偼婔傜偲應傟傞偱偟傚偆偐丅儗乕僓乕偺墲暅嫍棧偼丄廲曽岦偼2c/併(1-v2/c2)[m]丒墶曽岦偼2c/(1-v2/c2)[m]偲側傝傑偡丅埲壓偱丄偦偺巇慻傒傪夝愢偟傑偡丅
![併(c<sup>2</sup>-v<sup>2</sup>)[m/s]偱偁傞 廲墲暅偡傞岝偺憡懳懍搙](images/tatehoukounohikarinosoutaisokudo.jpg) 丂巹偲恀忋偵偁傞栚揑暔偼丄v[m/s]偱塃偵堏摦偟偰偄傑偡丅巹偼儗乕僓乕憰抲傪帩偭偰椢偺栴報偺捠傝堏摦偟傑偡丅儗乕僓乕偼丄愒偺栴報偺捠傝c[m/s]偱堏摦偟栚揑暔偵摉偨傝傑偡丅巹偑尒偨儗乕僓乕偺憡懳懍搙偼丄戞擇梋尫掕棟傛傝併(c2+v2-2cv*cos兤)[m/s]偲側傝傑偡丅廲曽岦偵偼cos兤=v/c側偺偱丄儗乕僓乕偺懍搙偼併(c2-v2)[m/s]偲側傝傑偡丅栚揑暔偵斀幩偟偰栠偭偰棃傞懍搙傕摨偠偱偡丅
丂巹偲恀忋偵偁傞栚揑暔偼丄v[m/s]偱塃偵堏摦偟偰偄傑偡丅巹偼儗乕僓乕憰抲傪帩偭偰椢偺栴報偺捠傝堏摦偟傑偡丅儗乕僓乕偼丄愒偺栴報偺捠傝c[m/s]偱堏摦偟栚揑暔偵摉偨傝傑偡丅巹偑尒偨儗乕僓乕偺憡懳懍搙偼丄戞擇梋尫掕棟傛傝併(c2+v2-2cv*cos兤)[m/s]偲側傝傑偡丅廲曽岦偵偼cos兤=v/c側偺偱丄儗乕僓乕偺懍搙偼併(c2-v2)[m/s]偲側傝傑偡丅栚揑暔偵斀幩偟偰栠偭偰棃傞懍搙傕摨偠偱偡丅
丂廬偭偰丄儗乕僓乕偑廲偵墲暅偡傞偺偵梫偡傞帪娫偼
2c[m]亐併(c2-v2)[m/s]=2/併(1-v2/c2) 昩
偱偡丅儗乕僓乕偺愨懳懍搙偼c[m/s]側偺偱丄廲曽岦偵儗乕僓乕偑墲暅偡傞幚嵺偺嫍棧偼
2/併(1-v2/c2) 昩亊c[m/s]=2c/併(1-v2/c2)[m]
偱偡丅
![(c-v)[m/s]偱偁傞 墶墲楬偺岝偺憡懳懍搙](images/yokoouronohikarinosoutaisokudo.jpg) 丂崱搙偼墶曽岦偱偡丅墶曽岦偺墲楬偼丄cos兤=1側偺偱丄墶墲楬偺岝偺憡懳懍搙偼(c-v)[m/s]偱偡丅
丂崱搙偼墶曽岦偱偡丅墶曽岦偺墲楬偼丄cos兤=1側偺偱丄墶墲楬偺岝偺憡懳懍搙偼(c-v)[m/s]偱偡丅
丂廬偭偰丄儗乕僓乕偑墶曽岦偺墲楬傪峴偔偺偵梫偡傞帪娫偼
c[m]亐(c-v)[m/s]=c/(c-v)昩
偱偡丅
![(c+v)[m/s]偱偁傞 墶暅楬偺岝偺憡懳懍搙](images/yokofukuronohikarinosoutaisokudo.jpg) 丂墶曽岦偺暅楬偼丄cos兤=-1側偺偱丄墶暅楬偺儗乕僓乕偺憡懳懍搙=(c+v)[m/s]偱偡丅
丂墶曽岦偺暅楬偼丄cos兤=-1側偺偱丄墶暅楬偺儗乕僓乕偺憡懳懍搙=(c+v)[m/s]偱偡丅
丂廬偭偰丄墶曽岦偺暅楬偵梫偡傞帪娫偼
c[m]亐(c+v)[m/s]=c/(c+v)昩
偱偡丅
丂屘偵丄墶曽岦偺墲暅偵梫偡傞帪娫偼
墶墲暅帪娫=c/(c-v)昩+ c/(c+v)昩=2/(1-v2/c2)昩
偱偡丅儗乕僓乕偺愨懳懍搙偼c[m/s]側偺偱丄
墶偺墲暅嫍棧=2/(1-v2/c2)昩亊c[m/s]=2c/(1-v2/c2)[m]
偱偡丅
丂偙傟偱丄巹偲栚揑暔偑v[m/s]偱暲憱偡傞偲丄廲偺墲暅嫍棧偼2c/併(1-v2/c2)[m]丒墶偺墲暅嫍棧偼2c/(1-v2/c2)[m]偲側傞偙偲偑暘偐傝傑偟偨丅
丂偮傑傝丄廲曽岦偼丄儗乕僓乕偼2/併(1-v2/c2)昩偱栠偭偰棃傑偡丅偟偐偟丄v[m/s]偱堏摦偡傞巹偺帩偭偰偄傞帪寁偼丄2/併(1-v2/c2)昩偵2昩傪崗傓條偵側傝傑偡丅廬偭偰丄巹偼廲曽岦偵墲暅偟偨儗乕僓乕偼2昩偱栠偭偰棃傞偲寁傝傑偡丅岝偺懍搙偼c[m/s]偲峫偊傞偺偱丄巹偲栚揑暔偲偺嫍棧偼丄2昩亊c[m/s]亐2=c[m]偲嶼弌偝傟傑偡丅
丂師偼墶曽岦偱偡丅墶曽岦偼儗乕僓乕偼2/(1-v2/c2)昩偱栠偭偰棃傑偡丅偟偐偟丄v[m/s]偱堏摦偡傞巹偺帩偭偰偄傞帪寁偼丄2/併(1-v2/c2)昩偵2昩傪崗傓條偵側傝傑偡丅廬偭偰丄巹偼墶曽岦偵墲暅偟偨儗乕僓乕偼2/併(1-v2/c2)昩偱栠偭偰棃傞偲寁傝傑偡丅岝偺懍搙偼c[m/s]偲峫偊傞偺偱丄巹偲栚揑暔偲偺嫍棧偼丄2/併(1-v2/c2)昩亊c[m/s]亐2=c/併(1-v2/c2)[m]偲嶼弌偟傑偡丅
丂偙偺條偵丄抶傟偨帪寁偲儗乕僓乕憰抲傪巊偆偲丄v姷惈宯偱偼丄墶曽岦偺嫍棧偼幚嵺傛傝傕1/併(1-v2/c2)攞挿偔應傟傞偺偱偡丅廲曽岦偱偼丄嫍棧偺曄壔偼偁傝傑偣傫丅廬偭偰丄嬻娫偺曄姺幃偼
嘇x'=x/併(1-v2/c2)
嘊y'=y
嘋z'=z
偲側傝傑偡丅偙傟偼丄儘乕儗儞僣廂弅偟偨掕婯傪巊偭偰挿偝傪應偭偨帪偲慡偔摨偠偱偡丅廬偭偰丄掕婯傪巊偭偰傕儗乕僓乕憰抲傪巊偭偰傕丄嫍棧偼偙偺條偵應掕偝傟傑偡丅
嘫.廬偭偰丄惓偟偄帪娫偲嬻娫偺曄姺幃偼師偺捠傝偱偁傞
丂廬偭偰丄帪娫偲嬻娫偺曄姺幃偼
嘆t'=t*併(1-v2/c2)
嘇x'=x/併(1-v2/c2)
嘊y'=y
嘋z'=z
偱偁傞偙偲偑暘偐傝傑偟偨丅
嘮.帪娫偲嬻娫偑偙偺條偵曄壔偡傞偲丄岝懍搙偼晄曄偲側傞
 丂帪娫偲嬻娫偑偙偺條偵曄壔偟偨帪丄岝偺懍搙偼婔傜偲應掕偝傟傞偱偟傚偆偐丅
丂帪娫偲嬻娫偑偙偺條偵曄壔偟偨帪丄岝偺懍搙偼婔傜偲應掕偝傟傞偱偟傚偆偐丅
丂偲偙傠偱丄岝傪捛偄偐偗偰偦偺懍搙傪應傞帠偼弌棃傑偣傫丅捠忢丄岝偺懍搙傪應掕偡傞応崌丄嬀傪巊偄岝傪斀幩偝偣偰丄岝偑栠偭偰棃傞偺偵梫偡傞帪娫傪寁傝傑偡丅岝偺墲暅嫍棧亐強梫帪娫傛傝丄岝偺懍搙傪寁嶼偟傑偡丅偦偆偡傞偲丄岝懍搙偼昁偢c[m/s]偲應掕偝傟傞偺偱偡丅埲壓偱偦偺巇慻傒傪愢柧偟傑偡丅
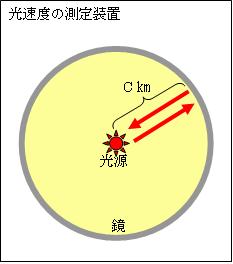
丂應掕憰抲傪丄敿宎c[m]偺媴懱偺撪柺嬀偲偟傑偡丅岝偼偦偺拞怱偐傜敪偟偰丄撪柺嬀偵斀幩偟偰嵞傃拞怱傊婣偭偰偒傑偡丅惷巭帪偵偼丄偁傜備傞曽岦傊敪偟偨岝偼丄慡偰2昩偱栠偭偰棃傑偡丅廬偭偰丄岝偺懍搙偼慡偰2c[m]亐2昩=c[m/s]偱偡丅
![慡偰2c/併(1-v<sup>2</sup>/c<sup>2</sup>)[m]偲側傞 岝偺墲暅嫍棧](images/hikarinooufukukyori2.jpg) 丂偱偼丄偙偺撪柺嬀偑v[m/s]偱堏摦偡傞偲丄岝偺懍搙偼婔傜偲寁傟傞偱偟傚偆偐丅撪柺嬀偼丄儘乕儗儞僣廂弅偟偰墶曽岦偵併(1-v2/c2)攞弅傒傑偡丅廲曽岦偺曄壔偼偁傝傑偣傫丅
丂偱偼丄偙偺撪柺嬀偑v[m/s]偱堏摦偡傞偲丄岝偺懍搙偼婔傜偲寁傟傞偱偟傚偆偐丅撪柺嬀偼丄儘乕儗儞僣廂弅偟偰墶曽岦偵併(1-v2/c2)攞弅傒傑偡丅廲曽岦偺曄壔偼偁傝傑偣傫丅
丂v[m/s]偱撪柺嬀偑堏摦偡傞偲丄儘乕儗儞僣曄姺廂弅偟側偗傟偽丄慜弎偺條偵丄岝偺墲暅嫍棧偼丄墶曽岦偱偼2c/(1-v2/c2)[m]偵丄廲曽岦偱偼2c/併(1-v2/c2)[m]偵側傝傑偡丅偟偐偟丄撪柺嬀偼儘乕儗儞僣廂弅偡傞偺偱丄墶曽岦偺墲暅嫍棧偼2c/(1-v2/c2)[m]亊併(1-v2/c2)= 2c/併(1-v2/c2)[m]偲丄廲曽岦偺墲暅嫍棧偲摨偠偵側傝傑偡丅偦偟偰丄岝偺愨懳懍搙偼c[m/s]偱偡丅廬偭偰丄岝偑弌敪偟偰拞怱偵栠傞偺偵梫偡傞帪娫偼丄2c/併(1-v2/c2)[m]亐c[m/s]=2/併(1-v2/c2)昩偲側傝傑偡丅
丂堦曽丄v[m/s]偱堏摦偡傞帪寁偼2/併(1-v2/c2)昩娫偵2昩傪崗傓條偵側傝傑偡丅偦偟偰丄惷巭帪偵偼丄撪柺嬀偺敿宎偼廲傕墶傕c[m]偱偡丅v[m/s]偱堏摦偡傞偲丄偙偺撪柺嬀偼墶曽岦偵併(1-v2/c2)攞廂弅偟傑偡丅偟偐偟丄掕婯傕墶偵併(1-v2/c2)攞廂弅偟傑偡丅屘偵丄v姷惈宯偱偼丄墶曽岦偺敿宎c*併(1-v2/c2)[m]傪c[m]偲掕媊偟傑偡丅廲曽岦偼丄撪柺嬀偼曄壔偟傑偣傫偟丄掕婯傕曄壔偟傑偣傫丅
丂廬偭偰丄v姷惈宯偱偼丄廲墲暅偟偨岝傕墶墲暅偟偨岝傕丄2昩娫偵2c[m]恑傫偩偲娤應偝傟傑偡丅廬偭偰丄岝偺憡懳懍搙偼忢偵2c[m]亐2昩=c[m/s]偲晄曄偲側傝傑偡丅
丂偙偺條偵丄憰抲帺懱偑儘乕儗儞僣廂弅偡傞偺偱丄岝懍搙偼忢偵晄曄偲側傝傑偡丅偱偼丄棧傟偨暔幙娫偱偼嫍棧偼曄壔偟傑偣傫偑丄偦偺娫偱岝傪墲暅偝偣偰岝偺懍搙傪寁傞偲丄婔傜偲側傞偱偟傚偆偐丅
丂巹偲栚揑暔偺嫍棧傪c[m]偲偟傑偡丅嘯偱愢柧偟偨捠傝丄儗乕僓乕偼丄廲墲暅偱偼2c/併(1-v2/c2)[m]傪2/併(1-v2/c2)昩偱栠傝傑偡丅偟偐偟丄v姷惈宯偺巹偑帩偭偰偄傞帪寁偼2/併(1-v2/c2)昩娫偵2昩傪崗傓偺偱丄儗乕僓乕偼2昩偱墲暅偟偰栠偭偰棃偨偲寁傟傑偡丅偙偺帪丄巹偼岝偺懍搙傪c[m/s]偲壖掕偡傞偺偱丄墲暅嫍棧傪c[m/s]亊2昩=2c[m]偲寁嶼偡傞偺偱偡丅廬偭偰丄曅摴偺嫍棧偼c[m]偲嶼弌偟傑偡丅
丂偙偺c[m](v姷惈宯偺)傪岝偼丄摉慠2昩(v姷惈宯偺)偱墲暅偟偰栠偭偰棃傑偡丅儗乕僓乕偲尵偆岝傪巊偭偰丄偦偺嫍棧傪媮傔偨偺偱偡偐傜丅廬偭偰丄岝偺懍搙偼2c[m]亐2昩=c[m/s]偲寁應偝傟傑偡丅
丂崱搙偼墶墲暅偱偡丅儗乕僓乕偼丄墶墲暅偱偼2c/(1-v2/c2)[m]傪2/(1-v2/c2)昩偱栠傝傑偡丅偟偐偟丄v姷惈宯偺巹偑帩偭偰偄傞帪寁偼2/併(1-v2/c2)昩娫偵2昩傪崗傓偺偱丄儗乕僓乕偼2/併(1-v2/c2)昩偱墲暅偟偰栠偭偰棃偨偲寁傟傑偡丅偙偺帪丄巹偼岝偺懍搙傪c[m/s]偲壖掕偡傞偺偱丄墲暅嫍棧傪c[m/s]亊2/併(1-v2/c2)昩=2c/併(1-v2/c2)[m]偲寁嶼偡傞偺偱偡丅廬偭偰丄曅摴偺嫍棧偼c/併(1-v2/c2)[m]偲嶼弌偟傑偡丅
丂偙偺c/併(1-v2/c2)[m](v姷惈宯偺)傪岝偼丄摉慠2/併(1-v2/c2)昩(v姷惈宯偺)偱墲暅偟偰栠偭偰棃傑偡丅儗乕僓乕偲尵偆岝傪巊偭偰丄偦偺嫍棧傪媮傔偨偺偱偡偐傜丅廬偭偰丄岝偺懍搙偼2c/併(1-v2/c2)[m]亐2/併(1-v2/c2)昩=c[m/s]偲寁應偝傟傑偡丅
丂埲忋偺條偵丄墲暅偱寁傞偲丄岝懍搙偼忢偵c[m/s]偲晄曄偲側傝傑偡丅偙傟偑丄乽岝懍搙晄曄偺尨棟乿偺巇慻傒偱偡丅
嘯.惓偟偄曄姺幃傪乽CATBIRD曄姺乿偲屇傇
丂廬偭偰丄岝懍搙偺曄姺幃偼
嘍c'=c
偱偡丅
丂嘆偐傜嘍傪傑偲傔傞偲丄帪娫丒嬻娫丒岝懍搙偺曄姺幃偼
嘆t'=t*併(1-v2/c2)
嘇x'=x/併(1-v2/c2)
嘊y'=y
嘋z'=z
嘍c'=c
偲側傝傑偡丅偙傟傪丄乽CATBIRD曄姺乿偲屇傇偙偲偵偟傑偡(2014/2/26丂PM23:38)丅
丂僩僢僾儁乕僕偱偼
嘐t'=t/併(1-v2/c2)
嘑c'=(c-vcos兤)
偲側偭偰偄傑偡丅偙傟偼丄曅摴偱峫偊偨曄姺幃偱偁傝丄墲暅偱峫偊傞偲忋婰嘆偐傜嘍偺捠傝偲側傝傑偡丅
丂嘐嘇嘊嘋嘑偺曄姺幃傪曅摴CATBIRD曄姺丒嘆嘇嘊嘋嘍偺曄姺幃傪墲暅CATBIRD曄姺偲屇傃傑偡丅
嘰.儅僀働儖僜儞偲儌乕儗乕偺憰抲傕儘乕儗儞僣廂弅偟偨偺偱丄岝偼摨帪偵栠偭偨
![c[m]傪墲暅偡傞 儅僀働儖僜儞偲儌乕儗乕偺幚尡憰抲](images/mmzikkennsouti.jpg) 丂岝偺憡懳懍搙傪嵟弶偵應掕偟偨偺偼丄儅僀働儖僜儞偲儌乕儗乕(埲壓丄MM偲尵偄傑偡)偱偡丅嬀傪巊偄曅摴11倣偺嫍棧傪墶曽岦偲廲曽岦偲偵墲暅偝偣傑偟偨丅偦偺寢壥丄忋婰偺巇慻傒偵傛傝丄2杮偺岝偼摨帪偵弌敪揰偵栠偭偰棃偨偺偱偡丅
丂岝偺憡懳懍搙傪嵟弶偵應掕偟偨偺偼丄儅僀働儖僜儞偲儌乕儗乕(埲壓丄MM偲尵偄傑偡)偱偡丅嬀傪巊偄曅摴11倣偺嫍棧傪墶曽岦偲廲曽岦偲偵墲暅偝偣傑偟偨丅偦偺寢壥丄忋婰偺巇慻傒偵傛傝丄2杮偺岝偼摨帪偵弌敪揰偵栠偭偰棃偨偺偱偡丅
丂MM憰抲偑儘乕儗儞僣廂弅偟側偗傟偽丄岝偺廲曽岦偺墲暅嫍棧偼22/併(1-v2/c2)倣丒墶曽岦偺墲暅嫍棧偼22/(1-v2/c2)倣偲側傝傑偡丅
丂崅懍堏摦偵傛傝丄MM憰抲偑墶曽岦偵併(1-v2/c2)攞廂弅偟偨偺偱偡丅偦偺堊偵丄岝偺墲暅嫍棧偼丄廲墶嫟偵22/併(1-v2/c2)倣偲側傝2杮偺岝偼摨帪偺栠偭偰棃偨偺偱偡丅偟偐偟丄儘乕儗儞僣偼丄暔幙偑僄乕僥儖偵墴偝傟偰廂弅偡傞偲峫偊傑偟偨丅偦偺偙偲傪棟榑揑偵夝柧弌棃偢丄僄乕僥儖偼斲掕偝傟傑偟偨丅
丂偟偐偟丄慜婰偺條偵丄棻巕娫偵摥偔堷椡偲愃椡偺曄壔傪峫偊傟偽丄暔幙偺廂弅傪愢柧偡傞偙偲偑弌棃傑偡丅
嘳.乽儘乕儗儞僣曄姺乿偑乽CATBIRD曄姺乿偲堎側傞偺偼壗屘偐
丂堦曽丄儘乕儗儞僣曄姺偼
嘍t'=(t-vx/c2)/併(1-v2/c2)
嘐x'=(x-vt)/併(1-v2/c2)
嘑y'=y
嘒z'=z
偱偡丅妋偐偵丄嬻娫偲帪娫偑偙偺條偵曄壔偡傟偽丄岝懍搙偼晄曄偲側傝傑偡丅
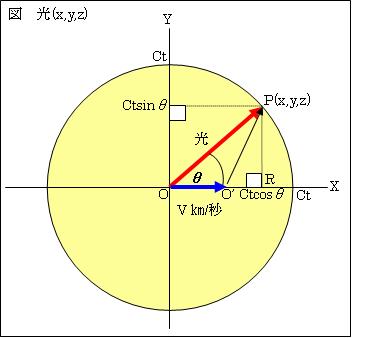 丂曄姺慜偺岝傪OP=嘓(x,y,z)= (ct*cos兤,ct*sin兤,0)偲偟(暯柺偱愢柧偟傑偡)丄曄姺屻偺岝傪O'P=(x',y',z')偲偟傑偡丅岝偼丄惷巭宯偱偁傞乽挻傂傕偺栐乿忋傪揱傢傝傑偡丅P偼丄尨揰O傪弌敪偟偨岝偺t昩屻偺埵抲偱偡丅
丂曄姺慜偺岝傪OP=嘓(x,y,z)= (ct*cos兤,ct*sin兤,0)偲偟(暯柺偱愢柧偟傑偡)丄曄姺屻偺岝傪O'P=(x',y',z')偲偟傑偡丅岝偼丄惷巭宯偱偁傞乽挻傂傕偺栐乿忋傪揱傢傝傑偡丅P偼丄尨揰O傪弌敪偟偨岝偺t昩屻偺埵抲偱偡丅
OP=併(x2+y2+z2)=併{( ct*cos兤)2+( ct*sin兤)+02}=ct[m]偱偡丅岝偼丄偙偺嫍棧傪t昩偱恑傒傑偡丅廬偭偰丄岝偺懍搙偼丄ct[m]亐t昩=c[m/s]偱偡丅
丂偱偼丄曄姺屻偺v姷惈宯偐傜尒偨岝偺堏摦偟偨嫍棧偼婔傜偲側傞偱偟傚偆偐丅偦傟偼丄崟偺栴報偺O'P偲側傝傑偡丅
丂岝偺X幉忋偺堏摦嫍棧O'R偼丄(ct*cos兤-vt)[m]偑1/併(1-v2/c2)攞偵怢傃傞偺偱丄(ct*cos兤-vt) /併(1-v2/c2)[m]偲尒偊傑偡丅x= ct*cos兤側偺偱丄(x-vt)/併(1-v2/c2)[m]偱偡丅
丂岝偺Y幉忋偺堏摦嫍棧偼丄曄壔偑側偄偺偱y[m]偱偡丅岝偺Z幉忋偺堏摦嫍棧傕丄曄壔偑側偄偺偱z[m]偱偡丅
丂廬偭偰丄岝偺恑傫偩嫍棧=O'P=併{((ct*cos兤-vt)/併(1-v2/c2))2+( ct*sin兤)2+02}=(c-vcos兤)t/併(1-v2/c2)[m]偱偡丅
丂岝偼O'P傪t昩偱恑傓條偵尒偊傑偡丅偟偐偟丄v姷惈宯偱偼丄偙偺t昩偼(t-vx/c2)/併(1-v2/c2)昩偲應掕偝傟傑偡丅x= ct*cos兤側偺偱丄t昩偼(c-vcos兤)t/c併(1-v2/c2)昩偲寁傟傑偡丅廬偭偰丄岝偺懍搙偼
(c-vcos兤)t/併(1-v2/c2)[m]亐(c-vcos兤)t/c併(1-v2/c2)昩=c[m/s]
偲晄曄偲側傝傑偡丅
丂偟偐偟丄GPS塹惎搵嵹偺帪寁偺抶傟偐傜偟偰傕丄帪娫偺曄姺幃偼丄嘆t'=t*併(1-v2/c2)偱偡丅寛偟偰嘍t'=(t-vx/c2)/併(1-v2/c2)偱偼偁傝傑偣傫丅傑偨丄岝偼偁偔傑偱傕乽挻傂傕偺栐乿忋偺OP傪恑傫偱偄傑偡丅寛偟偰O'P傪恑傫偱偄傞栿偱偼偁傝傑偣傫丅偨偩丄偦偆尒偊傞偩偗偱偡丅
丂儘乕儗儞僣曄姺偼丄堦懱壗傪昞偟偰偄傞偺偱偟傚偆偐丅幚偼丄儘乕儗儞僣曄姺偼丄v姷惈宯偱岝偺堏摦偟偨嫍棧偲帪娫傪媮傔傞幃側偺偱偡丅
丂岝偺X幉忋偺堏摦嫍棧偼丄(ct*cos兤-vt)[m]偱偡丅偟偐偟丄嬻娫偼CATBIRD曄姺偡傞偺偱丄v姷惈宯偱偼偦傟傪(ct*cos兤-vt)/併(1-v2/c2)[m]偲應傝傑偡丅Y幉忋偺堏摦嫍棧偼ct*sin兤[m]丄Z幉忋偺堏摦嫍棧偼0[m]偱偡丅
丂廬偭偰丄岝偺恑傫偩嫍棧偼丄併{((ct*cos兤-vt)/併(1-v2/c2))2+( ct*sin兤)2+02}=(c-vcos兤)t/併(1-v2/c2)[m]偱偡丅
丂t=1昩娫偱偼丄岝偺恑傫偩嫍棧=(c-vcos兤)/併(1-v2/c2)[m]偱偡丅岝尮偲嬀偺嫍棧傪丄偙偺2(c-vcos兤) /併(1-v2/c2)[m]棧偟丄嫟偵v[m/s]偱暲憱偝偣傑偡丅偦偟偰丄偦偺娫偵岝傪墲暅偝偣偰丄偦偺岝偺懍搙傪應掕偟偰尒傑偟傚偆丅彮乆暋嶨偱偡偑丄偙傟偑儘乕儗儞僣曄姺偺恀偺堄枴偱偡丅
岝偺墲暅偟偨嫍棧=2(c-vcos兤)/併(1-v2/c2)[m]
丂岝偺墲暅偵梫偟偨帪娫=2(c-vcos兤)/c併(1-v2/c2)昩偱偡丅偙傟偼丄儗乕僓乕憰抲偲CATBIRD曄姺偱抶傟偨帪寁傪巊偄丄偐偮儗乕僓乕偺懍搙傪c[m/s]偲壖掕偟偰嫍棧傪寁嶼偡傞偐傜偱偡丅墲暅帪娫亊c[m/s]=墲暅嫍棧偲嶼弌偡傞偺偱丄昁偢嫍棧亐c[m/s]=帪娫偲側傞偺偱偡丅偙偺弞娐榑朄偵傛傝丄岝懍搙偼昁偢2(c-vcos兤)/併(1-v2/c2)[m]亐2(c-vcos兤)/c併(1-v2/c2)昩=c[m/s]偲側傞偺偱偡丅
丂廬偭偰丄曅摴偺暯嬒傪弌偡偲
岝偺曅摴偵梫偟偨帪娫=t'=(c-vcos兤)t/c併(1-v2/c2)
X幉忋偺岝偺堏摦嫍棧=x'=(ct*cos兤-vt)/併(1-v2/c2)= (x-vt)/併(1-v2/c2)
Y幉忋偺岝偺堏摦嫍棧=y'=ct*sin兤=y
Z幉忋偺岝偺堏摦嫍棧=z'=0=z
丂X=ct*cos兤丄cos兤=x/ct偱偡丅屘偵
嘔t'=(c-vcos兤)t/c併(1-v2/c2)=(t-vx/c2)/併(1-v2/c2)
嘕x'=(ct*cos兤-vt)/併(1-v2/c2)= (x-vt)/併(1-v2/c2)
嘖y'=y
嘗z'=z
偲側傝丄儘乕儗儞僣曄姺偑摫偐傟傑偡丅廬偭偰丄儘乕儗儞僣曄姺幃偺恀偺堄枴偼丄v姷惈宯偱岝偺恑傫偩嫍棧偲帪娫傪昞偡傕偺側偺偱偡丅
侾侾.墲暅偱岝懍搙晄曄偱偁傟偽丄慡偰偺姷惈宯偱暔棟朄懃偼摨堦偲側傞
丂奆偝傫偼丄壗偩偲巚傢傟偨偙偲偱偟傚偆丅曅摴偺岝懍搙偑晄曄側偺偱偼側偔丄墲暅偝偣偰應傞偲岝懍搙偑晄曄偵側傞偺偱偡偐傜丅偟偐偟丄偙偺帠幚偼丄暔棟妛忋廳梫側堄枴傪帩偭偰偄傑偡丅偙偺巇慻傒偵傛傝丄慡偰偺姷惈宯偱暔棟朄懃偼摨堦偲側傞偺偱偡丅
丂抧媴偺懍搙偵墳偠偰丄廳椡偵傛傞棊壓懍搙傗丄揹帴婥椡偵傛傝暔懱偑摦偐偝傟傞懍搙偑曄傢傞偱偟傚偆偐丅幚嵺偵丄抧媴偼帺揮偟丄懢梲偺廃傝傪岞揮偟丄懢梲偼嬧壨偺拞傪岞揮偟偰偍傝丄嬧壨摨巑偼價僢僌僶儞偺敋敪偵傛傝丄崅懍偱墦偞偐偭偰偄傑偡丅抧媴偼戝曄暋嶨側壛懍尭懍塣摦傪偟偰偍傝丄抧媴偺愨懳懍搙偼忢偵暋嶨偵曄壔偟偰偄傞偲峫偊傜傟傑偡丅
丂偟偐偟丄抧媴偺堏摦懍搙偵娭學側偔丄忢偵摨偠嫮偝偺廳椡傗揹帴婥椡偑惗偠丄暔懱偼忢偵摨偠懍搙偱摦偐偝傟傑偡丅暔懱偺棊壓懍搙傪寁嶼偡傞廳椡掕悢傗儅僢僋僗僂僃儖偺曽掱幃偼丄抧媴偺堏摦懍搙傪慡偔峫椂偟偰偄傑偣傫丅偮傑傝丄抧媴偺堏摦懍搙偵娭學側偔丄岝偑恀嬻拞傪揱傢傞懍搙偼摨偠偱偁傝丄偦偺堊偵惗偠傞揹帴婥椡偺嫮偝偼晄曄偱偁傞偲偟偰偄傑偡丅偦偟偰丄尰幚偵晄曄側偺偱偡丅
丂偙傟偼壗屘偱偟傚偆偐丅揹帴婥椡偼丄揹壸傪懷傃偨暔幙娫傪揹帴攇偑墲暅偡傞偙偲偱惗偠傑偡丅揹壸傪懷傃偨2偮偺棻巕偑丄v[m/s]偱暪憱偟側偑傜揹帴攇傪岎姺偟崌偆偲丄慜婰偺條偵丄揹帴攇偺墲暅嫍棧偼廲1/併(1-v2/c2)攞丒墶1/(1-v2/c2)攞偵怢傃傑偡丅廬偭偰丄v姷惈宯偱偼惗偠傞揹帴婥椡偼庛傑傝偦偆偱偡丅
丂偟偐偟丄v[m/s]偱堏摦偡傞暔幙偼丄墶曽岦偵併(1-v2/c2)攞儘乕儗儞僣廂弅偟傑偡丅偙傟偱丄揹帴攇偺墲暅嫍棧偼廲墶嫟偵丄惷巭帪偵斾傋偰1/併(1-v2/c2)攞偺嫍棧偲側傝丄揹帴攇偑墲暅偡傞偺偵梫偡傞帪娫傕丄1/併(1-v2/c2)攞偲側傝傑偡丅偟偐偟丄帪寁偺恑傒曽傕丄1/併(1-v2/c2)攞偲備偭偔傝偲側偭偰偄傑偡丅廬偭偰丄揹帴攇偺墲暅偵梫偡傞帪娫偼惷巭帪偲摨偠偲寁傟傑偡丅偮傑傝丄岝偺懍搙偼晄曄偲側傝傑偡丅偦偺堊偵丄v姷惈宯偱偼丄惷巭帪偲摨偠揹帴婥椡偑惗偠偨偲娤應偝傟傞偺偱偡丅
丂廳椡傕摨條偱偡丅廳椡偼丄暔幙娫傪僌儔價僩儞偑岝懍偱墲暅偡傞偙偲偱惗偠傑偡丅揹帴婥椡偺応崌偲摨條偺尰徾偑婲偙傝丄慡偰偺姷惈宯偱偺棊壓偺曽掱幃偼摨堦偲側傞偺偱偡丅
丂棧傟偨暔懱摨巑偱偼偳偆偱偟傚偆偐丅暔懱摨巑c[m]棧偟偰尒傑偡丅偙偺娫傪揹帴攇偑墲暅偟傑偡丅廲曽岦偼丄忋婰偲摨偠偱偡丅墶曽岦偼丄c[m]傪c/併(1-v2/c2)[m]偲應傝傑偡丅墲暅偡傞偲丄2 c/併(1-v2/c2)[m]偱偡丅偦偟偰丄揹帴攇偼偦偺娫傪2c/(1-v2/c2)昩偱墲暅偟傑偡偑丄帪寁偑抶傟傞偺偱丄2c/併(1-v2/c2)昩偲寁傝傑偡丅廬偭偰丄岝偺懍搙偼c[m/s]偲惷巭帪偲摨偠偲側傞偺偱丄惗偠傞揹帴婥椡偺嫮偝傕惷巭帪偲摨偠偲娤應偝傟傞偺偱偡丅
丂偲偙傠偱丄惗偠傞揹帴婥椡偺嫮偝偼丄岝偺懍搙偵塭嬁偝傟傑偡丅岝偺懍搙偼恀嬻拞偑嵟傕懍偔丄暔幙拞偱偼抶偔側傝傑偡丅廬偭偰丄暔幙拞偱偼惗偠傞揹帴婥椡偼庛偔側傞偺偱偡丅忋婰偺捠傝丄堏摦偟偰傕揹帴攇偺懍搙偼晄曄側偺偱丄惗偠傞揹帴婥椡偺嫮偝傕晄曄偲娤應偝傟傞偺偱偡丅
侾俀.偦偆側傞偲摨帪惈偼憡懳揑偲側傞
![慡偰2c/併(1-v<sup>2</sup>/c<sup>2</sup>)[m]偲側傞 岝偺墲暅嫍棧](images/hikarinooufukukyori2.jpg)
丂僌儔價僩儞傗揹帴攇偑丄暔幙娫傪墲暅偡傞偺偵梫偟偨帪娫偵墳偠偨嫮偝偺廳椡傗揹帴婥椡偑惗偠傑偡丅偮傑傝丄壗帪憡庤偺棻巕偵僌儔價僩儞傗揹帴攇偑撏偄偨偺偐偼娭學側偄偺偱偡丅敿宎c[m]偺撪柺嬀傪巚偄弌偟偰壓偝偄丅岝偺敪幩偡傞妏搙偵傛傝丄偦偺岝偑撪柺嬀偵斀幩偟偨帪偼堎側傝傑偡丅偟偐偟丄慡偰偺曽岦傊敪偟偨岝偼丄惷巭帪偲摨偠帪娫偱栠偭偰棃傑偡丅廬偭偰丄慡偰偺曽岦偵偍偄偰惗偠傞廳椡傗揹帴婥椡偼晄曄偲娤應偝傟傞偺偱偡丅
丂曅摴偺岝懍搙偼丄晄曄偱偼偁傝傑偣傫丅偟偐偟丄堦乆暔幙偺廂弅偲岝懍搙偺曄壔傪媮傔偰丄惗偠傞揹帴婥椡偺嫮偝傪寁嶼偡傞偙偲偼柍懯偱偡丅寢壥偼摨偠側偺偱偡偐傜丄墲楬偲暅楬嫟偵岝懍搙偼晄曄偲壖掕偟偰丄暔棟寁嶼傪偟偨曽偑崌棟揑偱偡丅
丂偮傑傝丄憡庤偺棻巕偵僌儔價僩儞傗揹帴攇偺撏偄偨帪偼曽岦偵傛傝堎側傝傑偡偑丄偦傟傪摨帪偲偟偰暔棟寁嶼傪偟偰傕椙偄偙偲偵側傝傑偡丅偙傟傪乽摨帪惈偺憡懳惈乿偲尵偄傑偡丅
丂傑偨丄嫮偄廳椡偑帪寁偵妡偐傞偲丄帪寁傪峔惉偡傞棻巕偼摦偒擄偔側傝丄崅懍偱堏摦偟偨応崌偲摨條偺尰徾偑婲偙傝傑偡丅
侾俁.巹偺寢榑
巹偺摓払偟偨寢榑偼丄乽帪娫媦傃嬻娫帺懱偼曄壔偟側偄丅曄壔偡傞偺偼暔幙偺曽偱偁傞丅暔幙偑曄壔偡傞僗僺乕僪偑抶傟枖廂弅偡傞偺偱丄帪娫傗嬻娫偑曄壔偟偨條偵娤應偝傟傞丅乿偱偡丅
 丂暔幙傪峔惉偡傞棻巕摨巑偼丄偍屳偄偵愙偟崌偭偰偄傞栿偱偼偁傝傑偣傫丅棻巕娫偵摥偔堷椡偲愃椡偲偑掁傝崌偆堦掕嫍棧傪曐偭偰偄傑偡丅暔幙偑崅懍偱堏摦偡傞偲丄偙偺堷椡偲愃椡偺僶儔儞僗偑曄壔偟丄暔幙偼墶曽岦偵併(1-v2/c2)攞廂弅偡傞偺偱偡丅
丂暔幙傪峔惉偡傞棻巕摨巑偼丄偍屳偄偵愙偟崌偭偰偄傞栿偱偼偁傝傑偣傫丅棻巕娫偵摥偔堷椡偲愃椡偲偑掁傝崌偆堦掕嫍棧傪曐偭偰偄傑偡丅暔幙偑崅懍偱堏摦偡傞偲丄偙偺堷椡偲愃椡偺僶儔儞僗偑曄壔偟丄暔幙偼墶曽岦偵併(1-v2/c2)攞廂弅偡傞偺偱偡丅 丂傑偨丄尨巕婳摴傪夞傞揹巕摨巑偼偍屳偄偵斀敪偟崌偄傑偡丅偙偺條偵偟偰丄尨巕摨巑偼丄偦偺娫偵堷椡丒愃椡丒墦怱椡偑摥偒丄偦偺椡偺僶儔儞僗偺庢傟偨嫍棧傪曐偪側偑傜丄嫮偔寢崌偟偰偄傞偺偱偡丅
丂傑偨丄尨巕婳摴傪夞傞揹巕摨巑偼偍屳偄偵斀敪偟崌偄傑偡丅偙偺條偵偟偰丄尨巕摨巑偼丄偦偺娫偵堷椡丒愃椡丒墦怱椡偑摥偒丄偦偺椡偺僶儔儞僗偺庢傟偨嫍棧傪曐偪側偑傜丄嫮偔寢崌偟偰偄傞偺偱偡丅 丂偟偐偟丄幚嵺偵幙検偑憹壛偡傞栿偱偼偁傝傑偣傫丅v[m/s]偱堏摦偡傞暔幙偼丄惷巭帪偵斾傋偰併(1-v2/c2)攞偟偐摦偗側偔側傞偺偱丄偙偺條偵昞尰偡傞偺偱偡丅
丂偟偐偟丄幚嵺偵幙検偑憹壛偡傞栿偱偼偁傝傑偣傫丅v[m/s]偱堏摦偡傞暔幙偼丄惷巭帪偵斾傋偰併(1-v2/c2)攞偟偐摦偗側偔側傞偺偱丄偙偺條偵昞尰偡傞偺偱偡丅![併(c<sup>2</sup>-v<sup>2</sup>)[m/s]偱偁傞 廲墲暅偡傞岝偺憡懳懍搙](images/tatehoukounohikarinosoutaisokudo.jpg) 丂巹偲恀忋偵偁傞栚揑暔偼丄v[m/s]偱塃偵堏摦偟偰偄傑偡丅巹偼儗乕僓乕憰抲傪帩偭偰椢偺栴報偺捠傝堏摦偟傑偡丅儗乕僓乕偼丄愒偺栴報偺捠傝c[m/s]偱堏摦偟栚揑暔偵摉偨傝傑偡丅巹偑尒偨儗乕僓乕偺憡懳懍搙偼丄戞擇梋尫掕棟傛傝併(c2+v2-2cv*cos兤)[m/s]偲側傝傑偡丅廲曽岦偵偼cos兤=v/c側偺偱丄儗乕僓乕偺懍搙偼併(c2-v2)[m/s]偲側傝傑偡丅栚揑暔偵斀幩偟偰栠偭偰棃傞懍搙傕摨偠偱偡丅
丂巹偲恀忋偵偁傞栚揑暔偼丄v[m/s]偱塃偵堏摦偟偰偄傑偡丅巹偼儗乕僓乕憰抲傪帩偭偰椢偺栴報偺捠傝堏摦偟傑偡丅儗乕僓乕偼丄愒偺栴報偺捠傝c[m/s]偱堏摦偟栚揑暔偵摉偨傝傑偡丅巹偑尒偨儗乕僓乕偺憡懳懍搙偼丄戞擇梋尫掕棟傛傝併(c2+v2-2cv*cos兤)[m/s]偲側傝傑偡丅廲曽岦偵偼cos兤=v/c側偺偱丄儗乕僓乕偺懍搙偼併(c2-v2)[m/s]偲側傝傑偡丅栚揑暔偵斀幩偟偰栠偭偰棃傞懍搙傕摨偠偱偡丅![(c-v)[m/s]偱偁傞 墶墲楬偺岝偺憡懳懍搙](images/yokoouronohikarinosoutaisokudo.jpg) 丂崱搙偼墶曽岦偱偡丅墶曽岦偺墲楬偼丄cos兤=1側偺偱丄墶墲楬偺岝偺憡懳懍搙偼(c-v)[m/s]偱偡丅
丂崱搙偼墶曽岦偱偡丅墶曽岦偺墲楬偼丄cos兤=1側偺偱丄墶墲楬偺岝偺憡懳懍搙偼(c-v)[m/s]偱偡丅![(c+v)[m/s]偱偁傞 墶暅楬偺岝偺憡懳懍搙](images/yokofukuronohikarinosoutaisokudo.jpg) 丂墶曽岦偺暅楬偼丄cos兤=-1側偺偱丄墶暅楬偺儗乕僓乕偺憡懳懍搙=(c+v)[m/s]偱偡丅
丂墶曽岦偺暅楬偼丄cos兤=-1側偺偱丄墶暅楬偺儗乕僓乕偺憡懳懍搙=(c+v)[m/s]偱偡丅 丂帪娫偲嬻娫偑偙偺條偵曄壔偟偨帪丄岝偺懍搙偼婔傜偲應掕偝傟傞偱偟傚偆偐丅
丂帪娫偲嬻娫偑偙偺條偵曄壔偟偨帪丄岝偺懍搙偼婔傜偲應掕偝傟傞偱偟傚偆偐丅![慡偰2c/併(1-v<sup>2</sup>/c<sup>2</sup>)[m]偲側傞 岝偺墲暅嫍棧](images/hikarinooufukukyori2.jpg) 丂偱偼丄偙偺撪柺嬀偑v[m/s]偱堏摦偡傞偲丄岝偺懍搙偼婔傜偲寁傟傞偱偟傚偆偐丅撪柺嬀偼丄儘乕儗儞僣廂弅偟偰墶曽岦偵併(1-v2/c2)攞弅傒傑偡丅廲曽岦偺曄壔偼偁傝傑偣傫丅
丂偱偼丄偙偺撪柺嬀偑v[m/s]偱堏摦偡傞偲丄岝偺懍搙偼婔傜偲寁傟傞偱偟傚偆偐丅撪柺嬀偼丄儘乕儗儞僣廂弅偟偰墶曽岦偵併(1-v2/c2)攞弅傒傑偡丅廲曽岦偺曄壔偼偁傝傑偣傫丅![c[m]傪墲暅偡傞 儅僀働儖僜儞偲儌乕儗乕偺幚尡憰抲](images/mmzikkennsouti.jpg) 丂岝偺憡懳懍搙傪嵟弶偵應掕偟偨偺偼丄儅僀働儖僜儞偲儌乕儗乕(埲壓丄MM偲尵偄傑偡)偱偡丅嬀傪巊偄曅摴11倣偺嫍棧傪墶曽岦偲廲曽岦偲偵墲暅偝偣傑偟偨丅偦偺寢壥丄忋婰偺巇慻傒偵傛傝丄2杮偺岝偼摨帪偵弌敪揰偵栠偭偰棃偨偺偱偡丅
丂岝偺憡懳懍搙傪嵟弶偵應掕偟偨偺偼丄儅僀働儖僜儞偲儌乕儗乕(埲壓丄MM偲尵偄傑偡)偱偡丅嬀傪巊偄曅摴11倣偺嫍棧傪墶曽岦偲廲曽岦偲偵墲暅偝偣傑偟偨丅偦偺寢壥丄忋婰偺巇慻傒偵傛傝丄2杮偺岝偼摨帪偵弌敪揰偵栠偭偰棃偨偺偱偡丅 丂曄姺慜偺岝傪OP=嘓(x,y,z)= (ct*cos兤,ct*sin兤,0)偲偟(暯柺偱愢柧偟傑偡)丄曄姺屻偺岝傪O'P=(x',y',z')偲偟傑偡丅岝偼丄惷巭宯偱偁傞乽挻傂傕偺栐乿忋傪揱傢傝傑偡丅P偼丄尨揰O傪弌敪偟偨岝偺t昩屻偺埵抲偱偡丅
丂曄姺慜偺岝傪OP=嘓(x,y,z)= (ct*cos兤,ct*sin兤,0)偲偟(暯柺偱愢柧偟傑偡)丄曄姺屻偺岝傪O'P=(x',y',z')偲偟傑偡丅岝偼丄惷巭宯偱偁傞乽挻傂傕偺栐乿忋傪揱傢傝傑偡丅P偼丄尨揰O傪弌敪偟偨岝偺t昩屻偺埵抲偱偡丅