Top Pageへ
kothimaro変換とローレンツ変換の違いについて
ローレンツ変換
ローレンツ変換とkothimaro変換の違いについて述べます。
ローレンツ変換は次の通りです。
①x'=(x-vt)/√(1-v2/c2)
②y'=y
③z'=z
④t'=(t-vx/c2)/√(1-v2/c2)
⑤c'=c
xyzは空間の三次元、tは時間、cは光速度を表します。つまり、静止系の時空間(x,y,z,t)は、v慣性系では(x',y',z',t')={ (x-vt)/√(1-v2/c2),y,z, (t-vx/c2)/√(1-v2/c2)}に変換されると考えます。
正しい時間の変換式
一方、相対性理論の時間の変換式は
⑥t'=t*√(1-v2/c2)
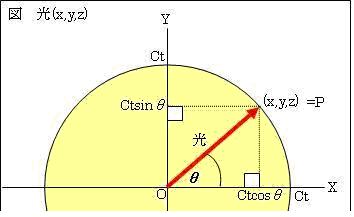
です。④と⑥が異なるのは何故でしょうか。その理由を、光を使って考えます。光をP(x,y,z)=(ct*cosθ,ct*sinθ,0)と平面で表します。静止系では、
光の移動距離=√(x2+y2+z2)=√{( ct*cosθ)2+( ct*sinθ)2+02}=ct[m]
光の移動時間=t秒
です。故に
光速度= ct[m]÷t秒=c[m/s]
となります。
kothimaro変換
では、この光をv[m/s]で移動する慣性系で観測すると、どうなるでしょうか。
v慣性系の光の移動距離=√(x'2+y'2+z'2)= √{(( ct*cosθ-vt)/√(1-v2/c2))2+( ct*sinθ)2+02}=⑩(c-v*cosθ)t/√(1-v2/c2)[m]
時間の変換式は⑥が正しいことが実証されています。従って
v慣性系の光の移動時間= t*√(1-v2/c2)秒
です。故に
v慣性系の光速度⑦c'=(c-v*cosθ)t/√(1-v2/c2)[m]÷t*√(1-v2/c2)秒=(c-vcosθ)/(1-v2/c2)[m/s]
となります。①②③⑥⑦をまとめると
①x'=(x-vt)/√(1-v2/c2)
②y'=y
③z'=z
⑥t'=t*√(1-v2/c2)
⑦c'=(c-vcosθ)/(1-v2/c2)
と、kothimaro変換となります。
光速度不変の原理
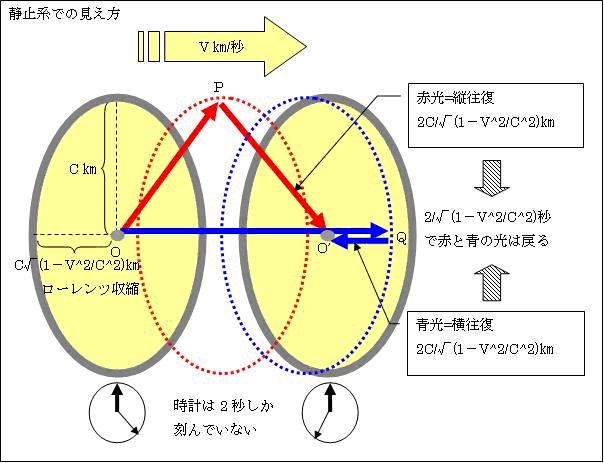kothimaro変換は、鏡で光を反射させ往復で速度を測定すると「光速度不変」になります。
v慣性系では、光の往復距離は横1/(1-v2/c2)倍・縦1/√(1-v2/c2)倍になります。但し、物質が横に√(1-v2/c2)倍ローレンツ収縮するので、横往復距離も1/√(1-v2/c2)倍となります。
一方、v[m/s]で移動する時計は√(1-v2/c2)倍ゆっくり時を刻みます。従って
v慣性系の光速度=c*√(1-v2/c2)/ √(1-v2/c2)=c[m/s]
と「光速度不変」になります。
これで、v慣性系でも電磁波は、静止時と同じ時間で物質間を往復する為、電磁力の強さは不変となります。これを「全ての慣性系で物理法則は同じ形となる」と言います。
一方、ローレンツ変換は、往路も復路も「光速度不変」とします。
⑩v慣性系の光の移動距離=(c-v*cosθ)t/√(1-v2/c2)[m]
です。光速度が不変なら
v慣性系の光の移動時間⑧t'=(c-v*cosθ)t/c*√(1-v2/c2)秒です。
これで、
v慣性系の光速度⑤c'=v慣性系の光の移動距離÷v慣性系の光の移動時間=(c-v*cosθ)t/√(1-v2/c2)[m]÷(c-v*cosθ)t/c*√(1-v2/c2)秒=c[m/s]
と光速度不変になります。
ローレンツ変換の導出方法
また、光の座標のX軸の値はx=ct*cosθなので、cosθ=x/ctです。これを⑧の時間の変換式に入れると、
光の移動時間t'=(c-vx/ct)t/c*√(1-v2/c2)秒=(t-vx/c2)/√(1-v2/c2)秒
です。従って、時間の変換式は
④t'=(t-vx/c2)/√(1-v2/c2)
です。
①②③④⑤をまとめると、「ローレンツ変換」となります。
光速度不変と特殊相対性原理
c[m]離れてv[m/s]で並走する物質ABが電磁波を交換します。実際には、ABが横並びと縦並びでは、Aの発した電磁波がBに到達した時は異なります。しかし、Aに戻って来た時は同じです。
ローレンツ変換は、往路も復路も光速度不変とするので、電磁波がBに到達した時は同時です。この為、ローレンツ変換では「同時性の相対性」が生じます。
この様に、kothimaro変換は、真実の時間・空間・光速度の変換を表現します。しかし、この形では、あらゆる方向へ向かう電磁波の往路と復路の時間を計算し合計しなければ、電磁力の強さは求められません。
一方、ローレンツ変換は、真実とは異なりますが、往路と復路共に光速度不変とするので、簡単に往復時間や電磁力の強さが計算出来ます。従って、実際の物理計算には、「ローレンツ変換」を使うのです。
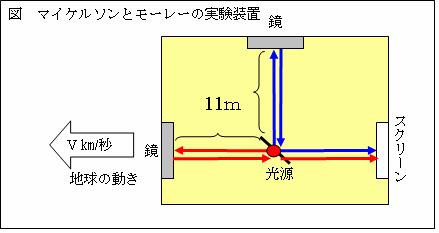
高速で移動すると、時間と空間の座標はどの様に変化するでしょうか。
マイケルソンとモーレーは、光を、地球の進行方向(横方向)とその上下左右方向(縦方向)に、鏡を使い片道11ｍの距離を往復させました。地球の速度はv[m/s]です。便宜上、片道を11ｍからc[m]にします。
横方向の往路では、光速度は(c-v)[m/s]です。∴それに要する時間はc/(c-v)秒です。横方向の復路では、光速度は(c+v)[m/s]です。∴それに要する時間はc/(c+v)秒です。つまり、往復に要する時間はc/(c-v)秒+ c/(c+v)秒=2c2/(c2-v2)=2/(1-v2/c2)秒です。光の絶対速度はc[m/s]なので、横方向の往復距離はc[m/s]×2/(1-v2/c2)秒=2c/(1-v2/c2)[m]です。
縦往復の往路と復路では、光速度はピタゴラスの定理より√(c2-v2)[m/s]となります。∴往復に要する時間は2c/√(c2-v2)秒=2/√(1-v2/c2)秒です。光の絶対速度はc[m/s]なので、縦方向の往復距離はc[m/s]×2/√(1-v2/c2)秒=2c/√(1-v2/c2)[m]です。
従って、横と縦に往復した2本の光は、同時には戻らない筈でした。しかし、実験の結果、同時に戻ったのです。これには、当時の物理学者は頭を抱えました。
そこで、ローレンツは、v[m/s]で移動する物質は進行方向に√(1-v2/c2)倍収縮すると考えました。これが、「ローレンツ収縮」です。これで、装置自体が横方向に√(1-v2/c2)倍収縮するので、光の横方向の往復距離は、2c*√(1-v2/c2)/(1-v2/c2)=2c/√(1-v2/c2)[m]と縦方向の往復距離と同じとなり、2本の光は同時に戻ることが出来ます。
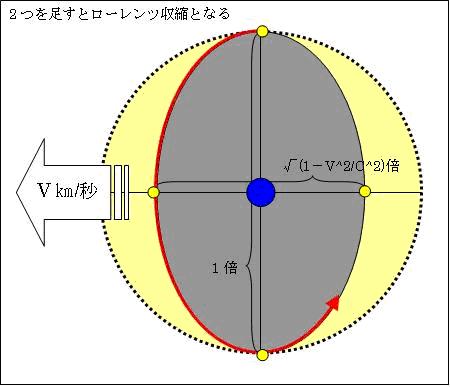アインシュタイン博士も、「ローレンツ収縮は妥当な解決策である」と述べられています。
原子が高速移動すると、電子が動き難くなり回転速度が落ち遠心力が弱まり原子核の電磁力に引かれ収縮するのです。この仕組みにより、v[m/s]で移動する物体は、進行方向に√(1-v2/c2)倍ローレンツ収縮します。
v慣性系では、物質である定規が横に√(1-v2/c2)倍収縮するので、距離は1/√(1-v2/c2)倍長く測定されます。その間、観測者自身がvt[m]移動しているので、その分短く測定されます。縦方向には変化はありません。∴
①x'=(x-vt)/√(1-v2/c2)
②y'=y
③z'=z
とローレンツ変換になります。
特殊相対性理論が提唱された理由
相対性理論は、「電磁気学の理論」として提唱されました。電磁気力は、電荷を帯びた物質間を、光の一種である電磁波が光速で往復することにより生じます。そして、生じる電磁気力の強さは、物質間の距離の2乗に反比例します。つまり、電磁波の往復に要する時間の2乗に反比例するのです。
v慣性系では、上記のとおり電磁波の往復距離は横1/(1-v2/c2)倍・縦1/√(1-v2/c2)倍となるため、生じる電磁気力の強さは弱まりそうです。しかし、実際にはその強さは変わりません。これを説明する為に、相対論が提唱されたのです。
v[m/s]で移動する地球上では、c[m]離れた物質間を、電磁波は縦も横も2/√(1-v2/c2)秒で往復することが分かりました。地球自身がローレンツ収縮するので、横往復距離が2c/√(1-v2/c2)[m]となるからです。
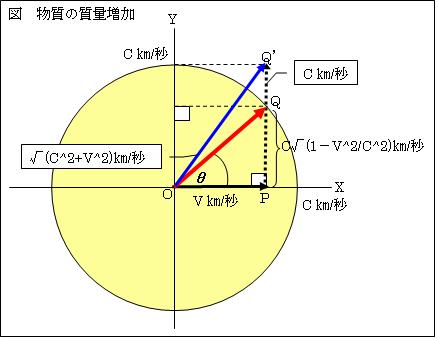一方、高速移動する物質は動かし難くなります。v[m/s]の粒子を、上下左右方向へ動かします。動かせる限度は√(c2-v2)[m/s]までです。この時、粒子の速度は、√{v2+(√(c2-v2))2}=c[m/s]とMAXとなります。
静止時には、c[m/s]まで動かすことが出来ました。∴v慣性系では、静止時の√(c2-v2)[m/s]÷c[m/s]=√(1-v2/c2)倍しか動かせないことが分かります。
この通り、高速で移動する時計の内部構造は、静止時に比べて√(1-v2/c2)倍しか動かないので、1秒間に√(1-v2/c2)秒を刻む様になります。これを、相対論では
④t'=t*√(1-v2/c2)
とします。
従ってv慣性系の時計は、電磁波が往復する2/√(1-v2/c2)秒間に2秒を刻みます。横方向の片道はc√(1-v2/c2)[m]に収縮していますが、定規も√(1-v2/c2)倍となっているので、これをc[m]と測定するのです。従って、
光の相対速度=2c[m]÷2秒=c[m/s]
と「光速度不変」となります。
v慣性系でも、静止時と同じ2秒で電磁波は往復するので、生じる電磁力の強さも同じなのです。これを「全ての慣性系において物理法則は同じ形となる」と言います。
正しい時間と空間の変換式
kothimaro変換は、①②③④で、正しい時間・空間・光速度の変換式を表しています。しかし、片道でも光速度不変を仮設すると、ローレンツ変換に変形されます。
kothimaro変換では、電磁波の往路と復路を変換して、それぞれに要する時間を求め合計しなければなりません。進行方向と電磁波の角度により無数の計算をする必要があり、事実上不可能です。
一方、ローレンツ変換は片道でも光速度不変となるので、全ての方向の電磁波の往復に要する時間をいとも簡単に求めることが出来ます。
この様に、ローレンツ変換は事実とは異なる仮設をすることにより、物理計算を可能にした偉大な発明です。
kothimaro変換は、正しい時間・空間・光速度の変化を表現します。実際の時間の変換式は、t'=t*√(1-v2/c2)なのですから。
この様に、実際には往路と復路とでは光の相対速度は異なります。しかし、光や電磁波を反射させて往復で測定すると、kothimaro変換では必ず「光速度不変」となります。
一方、電磁力は、電荷を帯びた物質間を電磁波が光速で往復することで生じます。生じる電磁力の強さは、電磁波の往復時間の2乗に反比例します。kothimaro変換では、電磁波が往復に要する時間は常に同じとなるので、v慣性系でも生じる電磁力の強さは不変なのです。
しかし、往路と復路に要する時間を算出し、合計するのは無駄です。それは常に同じなのですから。それなら、往路も復路も「光速度不変」と仮設した方が便利です。従って、kothimaro変換をローレンツ変換に変形して使うのです。
従って、実際にはローレンツ変換を使って物理計算をすべきです。
kothimaro変換の導き方
v[m/s]で移動する物質は、静止時に比べて√(1-v2/c2)倍しか動けません。従って、v[m/s]で移動する時計は、1秒間に√(1-v2/c2)秒を刻む様になります。v慣性系では、1秒間に光が進む距離をc[m]と定義します。従って、静止系で1秒間にc[m]進む光を、v慣性系では√(1-v2/c2)秒にc√(1-v2/c2)[m]進むと定義します。光の速度は、c√(1-v2/c2)[m]÷√(1-v2/c2)秒=c[m/s]です。即ち、v慣性系では、c[m]をc√(1-v2/c2)[m]と定義します。これを変換式で表わすと、
①t'=t√(1-v2/c2)
②x'=x√(1-v2/c2)
③y'=y√(1-v2/c2)
④z'=z√(1-v2/c2)
⑤c'=c
となります。これを「第一変換」と呼びます。
v慣性系では、進行方向には観測者自身がvt[m]移動しているので、その分距離は短く測定されます。上下左右方向には変化はありません。従って、空間の変換式は
x'=(x-vt)
y'=y
z'=z
です。静止系で1秒間にc[m]進む光をP(x,y,z)=(ct*cosθ,ct*sinθ,0)と平面で表します。その光は、v慣性系では、t秒間に√(x',y',z')[m]=ct√(c2+v2-2cv*cosθ)[m]進むと観測します。従って、光の速度はct√(c2+v2-2cv*cosθ)[m]÷t=c√(c2+v2-2cvcosθ)[m/s]です。従って、光速度は
c'= c√(c2+v2-2cvcosθ)
です。まとめると
⑥t'=t
⑦x'=(x-vt)
⑧y'=y
⑨z'=z
⑩c'=c√(c2+v2-2cvcosθ)
となります。これを「第二変換」と呼びます。
v[m/s]で移動する物質は、縦に√(1-v2/c2)倍・横に(1-v2/c2)倍収縮します。定規がこの様に収縮するので、距離は縦1/√(1-v2/c2)倍・横1/√(1-v2/c2)倍長く測定されます。この様に物質が収縮すると、物質間を電磁波が往復するのに要する時間は静止時と同じとなります。従って、物質の変化のスピードは不変です。従って
⑪t'=t
⑫x'=x/(1-v2/c2)
⑬y'=y/√(1-v2/c2)
⑭z'=z/√(1-v2/c2)
⑮c'=√(c+v* sinθ)*√(c-v* sinθ)/√(1-v2/c2)3
となります。これを「第三変換」と呼びます。
①から⑮を統合すると
⑯t'=t/√(1-v2/c2)
⑰x'=(x-vt)/√(1-v2/c2)
⑱y'=y
⑲z'=z
です。この時、光の進んだ距離=√(x',y',z')[m]=(c-vcosθ)t/√(1-v2/c2)[m]です。従って、光の速度=(c-vcosθ)t/√(1-v2/c2)[m]÷t/√(1-v2/c2)秒= (c-vcosθ)/ (1-v2/c2)[m/s]です。従って
⑳c=(c-vcosθ)/ (1-v2/c2)
となります。⑯⑰⑱⑲⑳を「kothimaro変換」と呼びます。
