「ニュートン力学」の正しい解釈

１.物質の運動を支配する法則の矛盾

　物質の運動を支配する基本法則には、ニュートン力学の「運動の第一法則」「運動の第二法則」「運動の第三法則」があります。しかし、これらの法則は、一見するとお互いに矛盾し合っていると思えます。

　「運動の第一法則」は、慣性の法則とも呼ばれます。これは外から力が加わらない限り、静止している物体は何時までも静止しており、等速運動する物体は何時までもその速度で同じ方向へ移動し続けるとの法則です。この速度を保とうとする性質を「慣性」と言います。

　加速度の大きさは、物体に加えた力の大きさに比例し、物体の質量に反比例します。これが「運動の第二法則」です。物体に加える力の大きさが2倍になると、その物体は2倍の速度で動き、物体の質量が2倍になるとその物体は1/2の速度で動きます。これを数式で表わすと、a=F/m (a=加速度・F=加える力・m=質量)です。

　運動する物体の持つ運動エネルギーは、質量に比例し速度の2乗に比例します。これが「運動の第三法則」です。物体の質量が2倍になると、この物体が衝突した時生じるエネルギーは2倍となり、速度が2倍となると衝突時のエネルギーは4倍となります。これを数式で表わすと、K=(1/2)mv² (K=運動エネルギー・m=質量・v=速度)です。

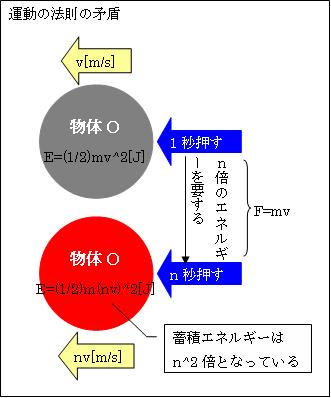　私には、この「運動に関する3つの法則」は、お互いに矛盾していると思えます。何故なら、運動エネルギーの足し算が成り立っていません。つまり、1+1=2となっていないのです。

　そのことを、詳説します。
　「運動の第二法則」によると、「�@n倍の時間同じ力Fを加える」と、物体Oの速度はn倍となります。しかし、「運動の第三法則」によると、速度がn倍になると運動エネルギーはn²倍となります。
　つまり、加えた力はn倍なのに、蓄積された運動エネルギーはn²倍になっています。私が物体Oを2倍の時間押せば、2倍のエネルギーを消耗します。私が、20[�s]の物体Oを持ってn秒歩くと、1秒歩いた時のn倍のエネルギーを消費します。
　ですから、�@のケースで加えた運動エネルギーはn倍です。しかし、蓄積された運動エネルギーはn²倍となっており、エネルギーが保存されていない様に思えます。

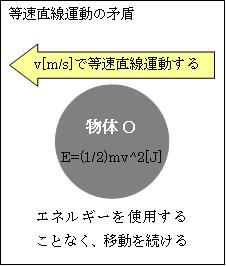　また私には、等速直線運動も「エネルギー保存の法則」に反する様に思えます。物体Oを1ｍ移動させると、必ずエネルギーを消費する筈です。しかし物体Oに一回力を加えると、その後物体Oは速度vで移動し続けます。つまり、物体Oはエネルギーを全く使わず移動しています。これらは、一体どう言うことでしょうか。

　これらは、初めて力学を学んだ際、誰もが感じる疑問であると思います。本HPでは、物体が動く仕組みを探求し、上記の疑問を解消して行きます。

２.波動で森羅万象を表わす。

　物理学では、森羅万象を「有の振動」で表し計算します。つまり有が光や物質粒子として振動するとそれが光や物質に見え、その振動が止むと真空に見えます。
　現在物理学では、「有」を、「超ひも」やそれが発展した「ブレーン」とします。百年以上前は、その「有」を「エーテル」と考えました。しかし、その「エーテル理論」は矛盾を含んでいた為に否定されました。同様に、現在の「超ひも」や「ブレーン」も、科学の進歩と共に止揚され、他の「概念」に置き換わるかも知れません。ですから本HPでは、それをただの「有」としておきます。

　以上のとおり、物質も光も「有の振動」です。「有の振動」は光速度cで伝わります。光としての波動は、何の抵抗も受けずそのまま光速度cで、有の中を伝わります。一方、物質には慣性力と言う抵抗が生まれ、光速度c未満でしか進めません。

３.万有引力

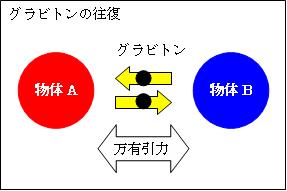　物体Aはグラビトンを発し、それを他の物体Bが吸収します。こうして、物体Aと物体Bはグラビトンを交換します。この仕組みにより、物体AB間に万有引力が働きます。

４.慣性力

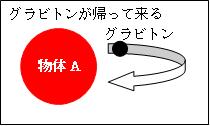　他の物体Bが無い場合、物体Aを構成する粒子から発せられたグラビトンは、その物体Aを構成する粒子に戻ります。

　物体Aを構成する粒子自体は、様々な方向へ光速度cで移動しようとします。しかし、お互いにグラビトンを交換し合い引き合うので、それぞれの力が打消し合い物体Aは静止しています。

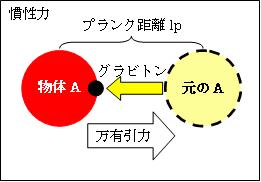　そして物体Aに力が加わり、それが少しでも特定の方向へ動くと、過去の自分が発したグラビトンを受け取るので、Aには元自分の在った方向へ万有引力が作用します。これが「慣性力」です。

　他の質量Bの万有引力に引かれる性質がAの「重力質量」であり、過去の自己の質量Aの万有引力に引かれる性質がAの「慣性質量」です。双方、万有引力によるので、「重力質量」と「慣性質量」の比率は全ての物質で同一です。

５.運動エネルギーの正体

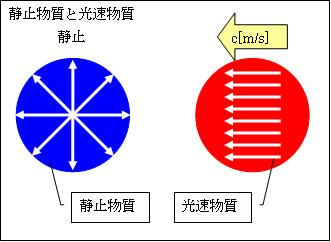
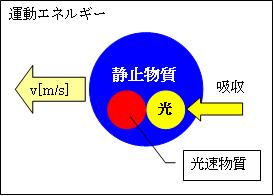　こうして、本来は光速度cで有を伝わろうとする物質波は静止しています。これを「静止物質」と言います。
　一方、１本の光は、同じ方向へ進む振動の集まりです。そして外の軌道に移る際、原子核を回る電子は光を吸収し速度を上げます。つまり物質の運動エネルギーの正体は、物質に吸収された光です。
　光は吸収されると、瞬間に同じエネルギーの静止物質の波動の方向を揃えます。すると、方向を揃えられた静止物質は、その方向へ光速度cで伝わる「光速物質」となります。速度vで等速直線運動する物体は「静止物質」と「光速物質」が一定の割合で混在しています。

６.プランク粒子の運動エネルギー

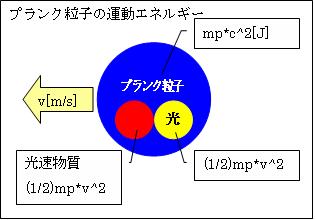　では運動の仕組みを、質量がプランク質量mpある「プランク粒子」を使って説明します。プランク粒子Pが1秒間でv[m/s]に達する加速度をv[m/s²]とします。
v[m/s]で進むプランク粒子Pの持つ運動エネルギーE=(1/2)mp*v²
です。したがって
�@光のエネルギーE =hf =(1/2)mp*v²=(1/2)Ep×(v²/c²)
の光が、質量mp[�s]の静止物質に吸収されると、瞬時にその中の(1/2)mp*v²=(1/2) (v²/c²)を持つ静止物質の進む方向が揃います。
　※h=プランク定数・f=周波数です。

７.運動エネルギーの伝播

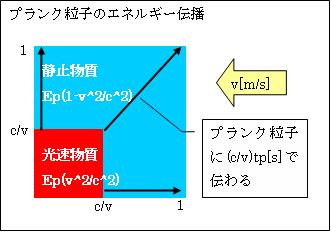　これに光自身のエネルギーを加えると、プランク粒子Pの(v²/c²)の割合が光速物質となります。残りの静止物質の割合は{1-(v²/c²)}です。この時
　プランク粒子の持つ運動エネルギーE=Ep (v²/c²)です。

　プランク粒子Pのエネルギー全体を、一辺が1の正方形で表します。すると、上記Ep(v²/c²)のエネルギーの物質波(以下、光速物質の波動を「光速波」と言います)は、一辺が(v/c)の正方形で表せます。 プランク粒子全体のエネルギー=Ep×1²=Epであり、光速波のエネルギー=Ep×(v/c)²=Ep(v²/c²)です。
　この一辺が(v*tp/c)の正方形の中に閉じ込められた波動は、(c/v)tp秒でプランク粒子P全体に伝わります。

８.粒子の移動

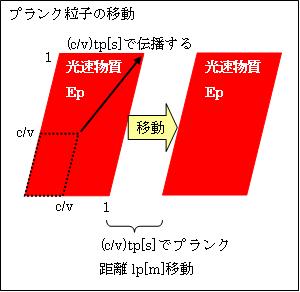　この光速波が、プランク粒子P内の静止物質に伝わると、その部分は光速物質となり、プランク距離lp進みます。つまり、波の速度は一定であり、静止物質が光速波になると、一瞬で速度0から速度cになります。こうして(c/v)tp秒で、プランク粒子P全体がプランク距離lp進みます。ですから
　プランク粒子Pの速度v=進んだ距離lp[m]÷進んだ時間(c/v)tp[s]=lp×tp×v÷c= c÷c×v=v[m/s]です。

９.光速物質の移動

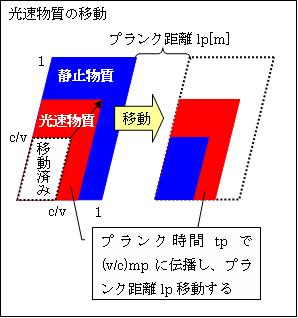　この様に、順次静止物質に光速波が伝わり、それが光速物質になりlp[m]進みます。そして、プランク距離lp進むと、過去の自分が発したグラビトンを、lpの至近距離で受け取ることになり、反対方向へ強い万有引力が働きます。これが「慣性力」です。

１０.慣性力の正体

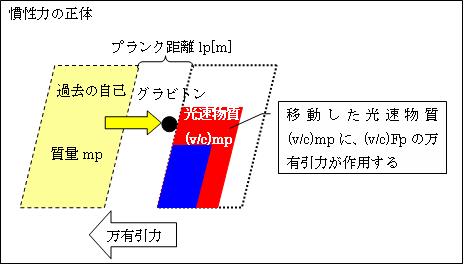　(c/v)tp秒で、プランク質量mp全体がlp[m]移動するので、説明を簡便にするために、プランク時間tpではmp×v/cの質量がlp移動すると仮設します。すると 自己の万有引力による慣性力(以下、抵抗力と言います)F1=G×mp×(v/c)mp÷lp²=G×√(h^ﾊﾞｰc/G)²×(v/c)÷√(h^ﾊﾞｰG/c³)²=c⁴/G×(v/c)=(v/c)Fp=プランク力Fpの(v/c)倍の力
です。
　※質量mpの過去の自分が発したグラビトンを、tp時間毎にlp移動した(v/c)mpの質量が受け取ります。ですからグラビトンを発する過去の自分の質量はmpであり、それを受け取る現在の自分の質量は(v/c)mpです。

１１.移動した光速物質の減速

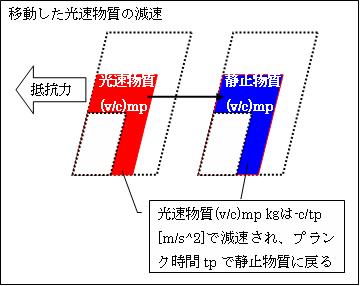　プランク力Fp=プランク質量×プランク加速度=mp×c/tpです。したがって
抵抗力F1=(v/c) mp×c/tp=mp*v/tp[N]
です。この様に抵抗力F1は、lp移動した(v/c)mpの質量を-c/tpで減速し、 tp[s]で光速度cから0に一気に減速します。つまり、光速物質となりtp[s]でlp[m]進んだ物質波は、自分が発したグラビトンにより、tp[s]で元の静止物質に戻ります。
　※プランク力Fp=c⁴/G、プランク質量mp=√(h^ﾊﾞｰc/G)、プランク加速度ap=Fp÷mp= c⁴/G÷√(h^ﾊﾞｰc/G)=√(c⁷/Gh^ﾊﾞｰ)=c√(c⁵/Gh^ﾊﾞｰ)=c/√(h^ﾊﾞｰG/c⁵)=c/tpです。

１２.プランク距離lp移動後の粒子の状態

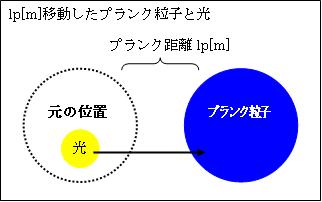　こうして、(c/v)tp 秒間でlp移動した質量mpの光速物質は、同じ(c/v)tp 秒間で光速度cから0に減速され、プランク粒子全てが元の静止物質になります。後に残ったのは、(1/2)mp*v²の光エネルギーのみです。この光が、lp進んだ静止しているプランク粒子に再吸収されます。

　そして最初に戻り、(1/2)mp*v² [J]の光エネルギーが同じエネルギーの静止物質を光速物質にして、光速物質はE×(v²/c²)になります。この運動エネルギーが(c/v)tp[s]で、プランク粒子P全体に広がりlp[m]進みます。そしてプランク粒子全体が、抵抗力F1により静止物質となり、後に(1/2)mp*v²の光エネルギーである運動エネルギーのみ残ります。その光エネルギーはlp先にある静止したプランク粒子Pに再吸収されます。これを繰り返すことで、プランク粒子Pは、lp÷(c/v)tp=v[m/s]で等速直線運動を続けます。

１３.粒子に掛かる推進力と抵抗力の釣り合い

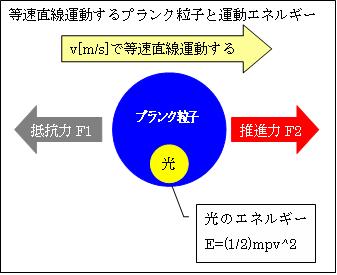　光速波は(c/v)tpで全体に伝わり、プランク粒子P全てが光速物質になり光速度cとなるので、その加速度はc÷(c/v)tp=v/tpです。したがって
プランク粒子Pの推進力F2=mp×v/tp[N]
です。この様に、プランク粒子の推進力F2=抵抗力F1となるので、両者の力が釣り合い、このプランク粒子Pはv[m/s]で等速直線運動をします。

１４.プランク粒子をmpv[N]でtp[s]間加速した時の運動エネルギー

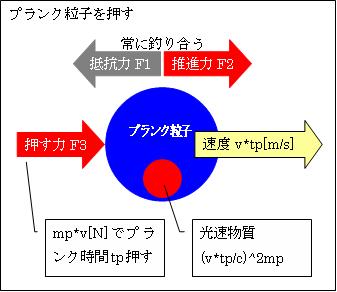　次に、プランク粒子Pを加速度a=v[m/s²]が生じる力で押し続けます。すると
押す力F3=mp*v=√(h^ﾊﾞｰc/G)×v[N]です。
　※このvは加速度であり、v[m/s²]です。

　この力でプランク時間tp押すと
プランク粒子Pの速度=at= v×tp=v*tp[m/s]
となります。この時
プランク粒子の運動エネルギーE=(1/2) mp (v*tp)²=(1/2)Ep(v*tp/c)²[J]
です。これが同じtp[s]で同量の静止物質を光速物質にするので、この時
プランク粒子Pの中の光速物質の割合={Ep×(v*tp/c)²}÷Ep=(v*tp/c)²
です。
　このまま同じ力でプランク粒子Pを押し続けます。すると、速度はどんどん上がり含まれる運動エネルギーが増えるので、推進力F2は大きくなって行きます。同時に抵抗力F1も同じだけ大きくなって行きます。つまり、幾ら推進力F2が大きくなり、tp[s]で多くの静止物質を光速物質に変えlp動かしても、同じ時間tp[s]で抵抗力F1によりその光速物質は静止物質に変えられます。ですから、推進力F2=抵抗力F1の関係は変わりません。

１５.運動エネルギーの伝播時間

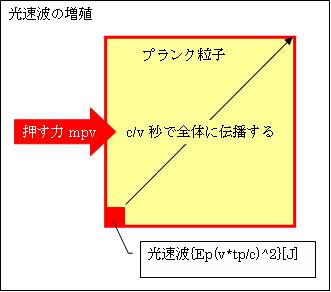　プランク粒子Pに掛かる推進力F2と抵抗力F1は常に釣り合うので、作用する力は押す力F3=mp*v=√(h^ﾊﾞｰc/G)×v[N]のみです。
　tp[s]で{Ep×(v*tp/c)²}[J]となった運動エネルギーである波動は、(c/v*tp)×tp=c/v秒で全体に伝わり、プランク粒子P全体を光速物質にします。この時、抵抗力F1は推進力F2により相殺されているので、それ以上の抵抗力による減速を考える必要はありません。

１６.粒子の加速

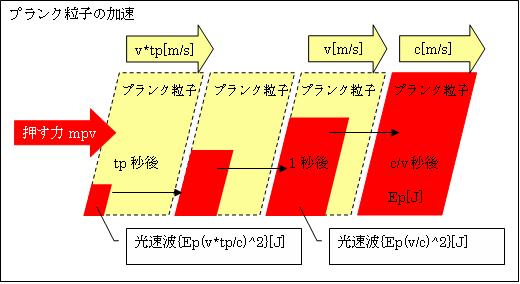　したがって、プランク粒子Pにmp*v[N]の力をc/v秒間加え続けると
プランク粒子Pの速度=at=v×c/v＝c[m/s]
と光速度cになります。つまり、プランク粒子P全体が光速物質になっています。プランク粒子Pはlp移動しながら、少しずつ光速物質が増えて行き、c/v秒で光速度cに達します。

１７.運動エネルギーの増殖

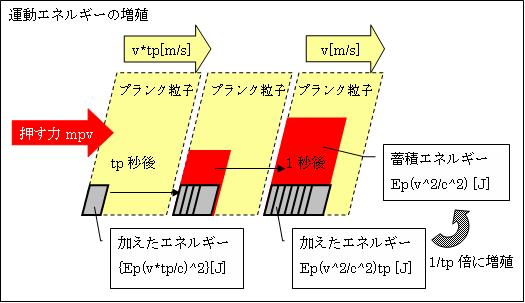　この様に、プランク粒子PをF3=mp*v[N]の力で押し続けると、tp[s]間で{Ep×(v*tp/c)²} [J]の運動エネルギーが与え続けられます。そして、F3の力で1秒間押し続けると
加えたエネルギー={Ep×(v*tp/c)²}×1/tp=Ep(v²/c²)tp [J]
です。しかし
1秒後のプランク粒子Pの速度=at=v
なので、プランク粒子P全体の(v²/c²)が光速物質となっています。つまり
1秒後のプランク粒子Pのエネルギー= Ep(v²/c²) [J]
です。このとおり、力F3を加え続ける限りプランク粒子P内の運動エネルギーは自ら増殖して行きます。つまり、F3が加え続けられると、tp[s]間で加えた{Ep×(v*tp/c)²}[J]の光速波がc/v秒で全体に伝わり、全てが光速物質となり、運動エネルギーは自ら増殖します。ですから、加えたエネルギー＜運動エネルギーとなります。

１８.運動エネルギーは保存する

　この様に、加えたエネルギーよりも存在する運動エネルギーの方が多いですが、それは静止物質が光速物質となっただけです。双方のエネルギーは同じです。ただ進む方向が光速物質では揃っているけれど、静止物質では揃っていないだけです。ですから、双方のエネルギー量は同じで、エネルギーは保存されています。

１９.衝突と物体の運動

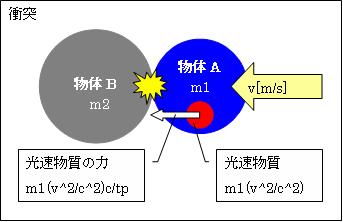次に、物体同士が衝突した時の運動を見て行きます。物体同士の「完全弾性衝突」の際、それらの運動量「P=mv」と運動エネルギー「E=(1/2)mv²」が保存されます。

静止している物体Bにv[m/s]で運動している物体Aが衝突します。そして、Bの質量をm2[�s]、Aの質量をm1[�s]とし、AとBの相対速度をvとします。すると、衝突後のAとBの相対速度は-v[m/s]となり保存されます。ここでは、Aの速度をv[m/s]、Bの速度を0[m/s]とします。この時、Aの中にある光速物質はm1(v²/c²)でした。したがって
物体Aの持つ力F=ma= m1(v²/c²)×c/tp= m1(v²/c²)c/tp[N]
です。

２０.作用と反作用

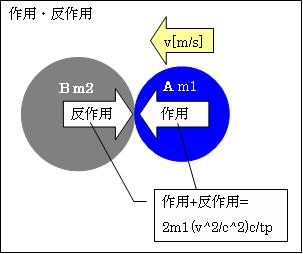AとBが衝突すると、作用反作用が生じるので、この力が2倍となります。したがって
衝突時に作用する力F'= 2×m1(v²/c²)c/tp[N]
です。

２１.AとBそれぞれに作用する力

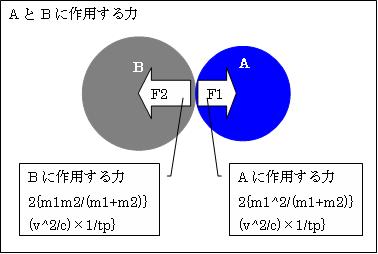この力F'を質量の大きさによりAとBが分け合います。つまり
物体Bに作用する力F'2=F'm2/(m1+m2) [N]
物体Aに作用する力F'1=F'm1/(m1+m2) [N]
となります。

２２.衝突後のBの速度

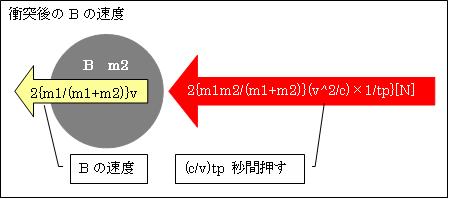したがって
物体Bに作用する力F'2=F'm2/(m1+m2)= {m2/(m1+m2)}{2×m1(v²/c²)×c/tp}=2{m1m2/(m1+m2)}(v²/c)×1/tp}[N]
物体Bの加速度a2=F'2/m2=2{m1/(m1+m2)}(v²/c)×1/tp}[m/s²]
です。
AとBの接触時間t=(c/v)tpなので
衝突後の物体Bの速度v2=a2t=2{m1/(m1+m2)}(v²/c)×1/tp}×(c/v)tp=2{m1/(m1+m2)}v[m/s]
です。

２３. 衝突後のAの速度

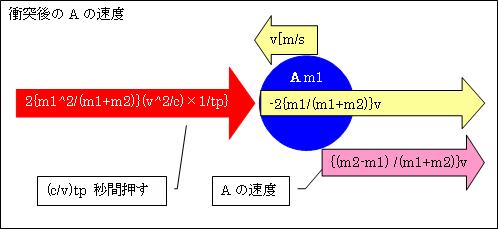一方
物体Aに作用する力F'1=F'm1/(m1+m2)= {m1/(m1+m2)}{ 2×m1(v²/c²)×c/tp}=2{m1²/(m1+m2)}(v²/c)×1/tp}
物体Aの加速度a1=F'1/m1=2{m1/(m1+m2)}(v²/c)×1/tp}
です。
AとBの接触時間t=(c/v)tpなので
衝突後の物体Aの変化速度v1=a1t=2{m1/(m1+m2)}(v²/c)×1/tp}×(c/v)tp=2{m1/(m1+m2)}v
です。したがって
衝突後の物体Aの速度v1'=v-v1=v-2{m1/(m1+m2)}v={1-2m1/(m1+m2)}v={(m1+m2-2m1) /(m1+m2)}v={(m2-m1) /(m1+m2)}v
となります。

衝突前のAとBの相対速度=0-v=-v
衝突後のAとBの相対速度v'=v2-v1=2{m1/(m1+m2)}v-{ (m2-m1) /(m1+m2)}v={(m1+m2)/(m1+m2)}v=v
と、衝突の前後で相対速度は反対向きになり絶対値は同じとなります。

２４.運動量保存の法則が成立する

次に、衝突の前後の運動量Pを計算します。
衝突前のAの運動量P1=m1v
衝突前のBの運動量P2=m2×0=0
です。∴
衝突前の運動量P= m1v+0= m1v
です。そして
衝突後のAの運動量P1'=m1v1=m1×{ (m2-m1) /(m1+m2)}v
衝突後のBの運動量P2'=m2×v2= m2×2{m1/(m1+m2)}v
です。∴
衝突後の運動量P'= P2'- P1' =m2×2{m1/(m1+m2)}v-m1×{(m2-m1)/(m1+m2)}v={(2m1m2-m1m2+m1²) /(m1+m2)}v={(m1+m2)/(m1+m2)}m1v=m1v
となります。つまり、衝突の前後で運動量は保存されます。

２５.運動エネルギー保存の法則が成立する

今度は、衝突の前後の運動エネルギーEを計算します。
衝突前のAの運動エネルギーE1=(1/2)m1v²
衝突前のBの運動エネルギーE2=(1/2)m2*0²=0
です。∴
衝突前の運動エネルギーE = (1/2)m1v²+0=(1/2)m1v²
です。そして
衝突後のAの運動エネルギーE1'=(1/2)m1v1'²=(1/2)m1{ (m2-m1) /(m1+m2)}²*v²
衝突後のBの運動エネルギーE2'=(1/2)m2v2'²=(1/2)m2{2m1/(m1+m2)}²*v² です。∴
衝突後の運動エネルギーE'
=E1'+ E2'=(1/2)m1{ (m2-m1) /(m1+m2)}²*v²+(1/2)m2{2m1/(m1+m2)}²*v²
=(1/2){v²/(m1+m2)²}{m1(m2²-2m1m2+m1²)+m2(4m1²)}
= (1/2){v²/(m1+m2)²}(m1m2²-2m1²m2+m1³+4m1² m2)
=(1/2){m1*v²/(m1+m2)²}(m2²-2m1m2+m1²+4m1m2)
=(1/2){m1*v²/(m1+m2)²}(m1²+2m1m2+m2²)= (1/2){m1*v²/(m1+m2)²}(m1+m2)²=(1/2)m1v²
となります。つまり、衝突の前後で運動エネルギーは保存されます。