Top Page CATBIRD挨拶
第一部光速度不変の原理
第二部ニュートン力学
第三部超ひも理論
第四部電磁気力
第五部一般相対性理論
第六部精神の力
第七部神の力
第八部波動一元論
「光速度不変の原理」と「特殊相対性理論」の正しい解釈
１.高速移動に伴う変化
私が高速で移動すると、一体何が起こるでしょうか。常識からすれば、他の物の相対速度(自分から離れて行く速度と自分に近づいて来る速度)が変化するだけです。時間の経過も空間の長さも変わるとは思えません。しかしこれは、低速で移動した時の体験からそう思うのです。
光速度である299,792,458[m/s](以下、c[m/s]と言います)が、あらゆるものの速度の上限と考えられています。この速度に近づくと、時間の経過が遅れ、空間は進行方向に伸びます。しかし、光の相対速度はc[m/s]で変わらないと考えられています。
つまり、光と対面する形で高速移動しながら光が自分に近づいて来る速度を測っても、光と並走する形で光が自分から離れて行く速度を測っても、その相対速度は常にc[m/s]としか測れないとされています。
しかし、これは常識に反するため大変理解し難いです。このホームページでは、高速移動により時間と空間の「座標」が変化する仕組みを説明します。そして、現実には光速度は不変ではないことも解説します。それと同時に、何故「光速度不変」を仮設して、物理計算をしなければならないのかその理由も述べます。
先ず、本HPの要旨を概説します。
電磁気力は、荷電粒子間を光の一種である電磁波が往復することで生じます。2つの荷電粒子αとβがv[m/s]で移動しながら電磁波を交換すると、その往復距離は伸びます。ですからv慣性系では、生じる電磁気力は弱まると思えます。
しかし現実には、荷電粒子と同じ動きをする観測者Aに、電磁気力の強さは静止時と同じと見えます。
この難問を解決するためにアインシュタイン博士は、「光速度不変の原理」を提唱されました。つまり、粒子αとβ及び観測者Aのどちらから見ても、往復運動する電磁波の相対速度(αβAから離れて行く速度又はαβAに近づいて来る速度)は光速度cで不変であると仮設されました。
そして、光の相対速度がcで不変となる様に、αβAの時間と空間が連動して「ローレンツ変換」すると思考されました。これが「特殊相対性理論」です。
これで粒子αβ観測者A誰から見ても、電磁波は静止時と同じ時間で往復して見えます。ですから、vで移動する粒子αβ間に生じる電磁気力の強さは、静止時と同じで不変です。
しかし、時間と空間の中には何もありません。「中に何も無いものが変化する仕組み」は未来永劫説明することは出来ません。何しろ、説明に使う材料が何もないのですから。
ですから、物理現象は時間と空間を変化させるのではなくて、物質の方を変化させて説明しなければなりません。
光速度cに近づくにしたがって、粒子は動き難くなります。これは加速器の実験で実証済みです。ですから、高速で運動する時計を構成する粒子は動き難くなり、その時計は遅れます。高速で運動する定規を構成する原子核の周りを公転する電子も動き難くなります。ですから、電子の公転速度は落ち、電子に掛かる遠心力は弱まります。したがって、電子は原子核の電磁気力に引かれて、より小さい軌道を公転します。この仕組みにより、vで移動する定規は収縮します。
この遅れた時計と収縮した定規を使い、鏡で反射させた光の往復での平均速度を測定すると、移動速度vやαβAの移動方向と光の伝わる方向との角度θにかかわらず、必ず光の相対速度は光速度cと測定されます。
そして、時計が遅れ定規が収縮するので、v慣性系の時間と空間の座標は変化します。この変換式を「CATBIRD変換」と言います。
電磁気力は電磁波が往復して生じるので、往復での平均速度が光速度cなら、電磁波は静止時と同じ時間で荷電粒子間を往復します。これで、vで移動する粒子間に働く電磁気力の強さは静止時と同じになります。
しかし、あらゆる方向へ進む電磁波を、往路と復路に分けて「CATBIRD変換」で計算することは事実上不可能です。そこで、片道でも光速度不変と仮設したのが、特殊相対性理論の基礎となる「ローレンツ変換」です。
電磁気力は電磁波が往復することで生じるので、片道で光速度不変と仮設しても、物理計算上何ら問題はありません。
こう言う意味で、「光速度不変の原理」は物理計算を可能にした偉大な発明です。以下で、この内容を詳説して行きます。
２.なんとも不思議な「光速度不変の原理」
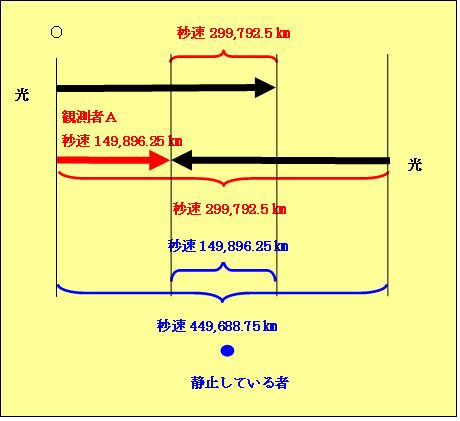今、観測者Aが光の相対速度を測定しようとしています。Aが静止していれば、どの方向に向かう光も、秒速299,792,458[m/s]で自分に近づき、又は自分から離れて行くと見えます。
では、観測者Aが左図の赤い矢印の様に、光速度cの半分の速さの149,896,229[m/s]で右に移動しながら、上の黒い矢印で表した同じ方向へ進む光の相対速度(Aから離れる速度)を観測すると、幾らと測れるでしょうか。常識的には、上の黒い矢印で表した光の相対速度は、299,792,458[m/s]-149,896,229[m/s]=149,896,229[m/s]と測れると思うでしょう。
では、観測者Aが同じ運動をしながら、今度は下の黒い矢印で表した自分に向かって来る光の相対速度(Aに近づく速度)を観測したらどうでしょうか。Aはその光を、299,792,458[m/s]+149,896,229[m/s]=449,688,687[m/s]と測るでしょうか。
現代物理学では、この我々の常識に反して、観測者Aにはどちらの光の相対速度も299,792,458[m/s](光速度c)としか測れないとします。つまり、観測者Aがどの様な速さで移動しながら、どの方向へ向かう光の相対速度を計っても、その光は光速度cで自分から離れて行き、又は自分に近づいて来るとしか測れないと言うのです。
Aが亜光速で移動しながら並走する光を計っても、逆に光自分に向かってくる光を計っても、その光の相対速度はcとしか測ることが出来ません。つまり、自分と並走する光を見ると自分の時間は遅れ空間は縮み、自分と対面する光を見ると自分の時間は速く進み空間は伸びます。
では、併走する光と対面する光を同時に見たら、私に流れる時間や私の空間はどの様に変化するのでしょうか。また、どの光も見ずに目を瞑ったら、私の時間や空間はどの様に変化するのでしょうか。更にこれでは、時間や空間は観測者の数だけ複数あることになります。つまり、観測者が新たに生まれたら、その人用の時間と空間が用意されるのです。
この様に我々の常識からすると、「光速度不変の原理」は矛盾していると思えます。
３.ローレンツ変換について
まず始めに、ローレンツ変換について触れておきます。ローレンツ変換は、特殊相対性理論の基礎となる時間と空間の変換式です。それは、「光速度不変の原理」を前提とし、v[m/s]で移動する慣性系では、時間と空間は次の通り光の相対速度が不変になる様に連動して変化すると考えます。
v=観測者Aの移動速度、x=進行方向の移動距離、yとz=進行方向に向かって上下左右の方向の移動距離、t=経過時間、c=光の速度です。
①x'=(x-vt)/√(1-v2/c2) (観測者Aがvt[m]移動した分空間は収縮する。また、1/√(1-v2/c2)倍空間は伸びる)
②y'=y (変化しない)
③z'=z (変化しない)
④t'=(t-vx/c2) /√(1-v2/c2 (空間と連動し、「光速度不変」となる様に奇妙な変化をする)
⑤c'=c (光速度不変の原理)
次に、ローレンツ変換の考え方を説明します。物質は、電磁力・重力・強い力・弱い力の4つの力により動きます。ローレンツは、光と重力及び電磁力は光速で「エーテル」の中を伝わり、物質は「エーテル」の中をv[m/s]で動くと考えました。その当時、強い力と弱い力はまた発見されていませんでした。また、重力と電磁力は直線的に光速で伝わると考えられていました。
物質を動かす重力と電磁力が速く伝われば、物質を構成する粒子は速く動きます。そうなると、私の持っている時計は速く時を刻みます。私も、速く動き・速く思考し・早く年を取ります。
逆に、物質を動かす力が遅く伝われば、物質を構成する粒子の動きは遅くなります。そうなると、私の持っている時計はゆっくりと時を刻みます。私は、ゆっくりと動き・ゆっくりと思考しゆっくりと年を取ります。
したがって、物質が時を刻むスピードは、物質が発した重力及び電磁力が隣の物質へ直線的に到達するのに要する時間に反比例すると考えました。
※現在では、「ゲージ粒子」が光速度cで物質間を往復することにより、4つの力は生じるとされています。従って、物質が変化するスピードは、「ケージ粒子」が物質間を往復するのに要する時間に反比例します。
物質を動かす力と光が同じ速度で伝わる限り、観測される光の速度は不変です。例えば、私がc/2[m/s]で光と並走する時、光の相対速度(光が自分から離れて行く速度)がc/2[m/s]となっても、その方向へ物質を動かす力が伝わる速度もc/2[m/s]となります。その結果、私の体を構成する物質の動きは1/2倍遅くなります。私の持っているあらゆる時計も、その動きは1/2倍遅くなります。
私にとって時間の経過は、2倍とゆっくりしたものになります。私が1秒と考える時間の間隔は、実際の2秒となります。その時、私の観測する光の相対速度は、c/2[m/s]×2秒=c[m/s]で不変です。
４.ローレンツ変換の導き方
では、ローレンツ変換の導き方を説明します。
ある物質Oから発せられた物質を動かす力が、c[m]離れた隣の物質Pに到達するのに要する時間は、その力が伝わる速度がc[m/s]とすると、静止時ではc[m]÷c[m/s]=1秒です。
v[m/s]で移動する慣性系(以下、v慣性系と言う)では、第二余弦定理により
物質を動かす力の伝播速度=⑧√(c2+v2-2cv*cosθ)[m/s]
となります。
※以下で、便宜上物体間の距離をc[m]と仮設して度々説明します。
従って、物質Oが発した物質を動かす力が、c[m]離れた物質Pに届くのに要する時間は、 c/√(c2+v2-2cv*cosθ)秒です。 静止時には1秒で届きました。したがってv慣性系では、物質が同じ動きをするのに、静止時のc/√(c2+v2-2cv*cosθ)倍の時間が掛かります。したがってv慣性系の時計は、1秒間に√(c2+v2-2cv*cosθ)/c秒を刻みます。∴時刻は
⑥t'=t√(c2+v2-2cv*cosθ)/c
と変換されます。
進行方向であるX軸方向へは、観測者Aがvt[m]移動した分、距離が収縮した様に観測されます。したがって、X軸方向は
⑦x'=x－Vt
となります。Y軸Z軸方向は変化しません。従って、空間と時間の変換式は
⑦x'=x－Vt
③y'=y
④z'=z
⑥t'=t√(c2+v2-2cv*cosθ)/c
となります。これを「第一変換」と呼びます。
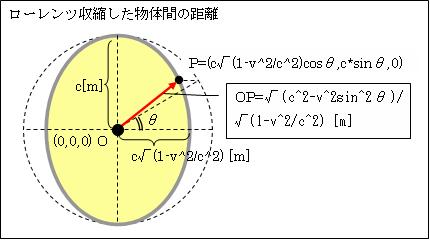vで移動する物体は、進行方向へ√(1-v2/c2)倍収縮します。上下左右方向には変化しません。これを「ローレンツ収縮」と言います。ローレンツは「エーテル」の抵抗を受けて物質がこの様に収縮すると考えました。これはマイケルソンとモーレーの実験により確認されました。その詳細は、下記で説明します。
V慣性系の定規は「ローレンツ収縮」するので、距離は逆に1/√(1-v2/c2)倍長く測れます。したがって、X軸方向は
⑧x'=x/√(1-v2/c2)
となります。
Y軸Z軸方向は変化しません。従って、空間の変換式は
⑧x'= x/√(1-v2/c2)
③y'=y
④z'=z
です。
vで移動する地球全体が「ローレンツ収縮」するので、物体Oと隣の物体Pの距離は、c[m]から次のとおり変化します。Oを原点(0,0,0)とするとc[m]離れたPの座標は(c*cosθ,c*sinθ,0)と表せます。したがって
OP間の距離=√(x'2+y'2+z'2)=√[{x/√(1-v2/c2)}2+y2+02]= √[{ c*cosθ/√(1-v2/c2)}2+(c*sinθ)2+02)]=√(c2-v2sin2θ)/ √(1-v2/c2) [m]です。
そして、物質を動かす力はc[m/s]で伝わるので
力がOP間を進む時間=√(c2-v2sin2θ)/ √(1-v2/c2) [m]÷c[m/s]= √(c2-v2sin2θ)/ c√(1-v2/c2)[s]
です。
地球全体が「ローレンツ収縮」すると、物質間の距離c[m]がこの様に変化し、物質を動かす力が到達するのに要する時間が1[s]から√(c2-v2sin2θ)/c√(1-v2/c2)[s]になりました。したがって、物質が変化するスピードは、c√(1-v2/c2)/√(c2-v2sin2θ)倍になります。したがって、時計が刻む時刻は
⑥t'=tc√(1-v2/c2)/√(c2-v2sin2θ)
となります。これを「第二変換」と呼びます。
「第一変換」と「第二変換」を合わせると
⑨x'=(x-vt)/√(1-v2/c2)
③y'=y
④z'=z
となります。この時、P=(x,y,z)=(ct*cosθ,ct*sinθ,0)なので、これを⑨③④を使って変換すると、P' (x',y',z')={(ct*cosθ-vt)/√(1-v2/c2), ct*sinθ,0}となります。したがって
OP間の距離=√(x'2+y'2+z'2)= √[{(ct* cosθ-vt)/√(1-v2/c2)} 2+(ct*sinθ)2]
= t√{(c* cosθ-v)2*(c2/c2-v2)+c2 sin2θ}
= t√{(c2cos2θ-2cv*cosθ+v2)*(c2/c2-v2)+(c2*sin2θ-v2 sin2θ) *(c2/c2-v2)}
= t√{(c2/c2-v2) (c2cos2θ-2cv*cosθ+v2+c2sin2θ-v2 sin2θ) }
=t√{(c2/c2-v2) (c2-2cv *cosθ+v2-v2(1- cos2θ) }
=t√{(c2/c2-v2) (c2-2cv *cosθ+v2-v2+v2cos2θ) }
=t√{(c2/c2-v2) (c2-2cv *cosθ+v2cos2θ) }
=t√{(c2/c2-v2) (c-v*cosθ) 2}
=(c-v*cosθ)t/√(1-v2/c2) [m]
です。
物質を動かす力が伝わる速度はc[m/s]なので
⑩力がOP間を進む時間=(c-v*cosθ)t/√(1-v2/c2) [m]÷c[m/s]= (c-v*cosθ)t/c√(1-v2/c2) [s]
です。
PのX軸の座標x=ct*cosθなので、cosθ=x/ctです。これを⑩に代入すると
④t'=(c-v*cosθ)t/c√(1-v2/c2)= (c-vx/ct)t/c√(1-v2/c2)=(t-vx/c2) /√(1-v2/c2)
です。まとめると
①x'=(x-vt)/√(1-v2/c2)
②y'=y
③z'=z
④t'=(t-vx/c2) /√(1-v2/c2）
と「ローレンツ変換」になります。
５.ローレンツ変換による光速度不変の原理の説明
ではこの「ローレンツ変換」で、実際に光速度が不変となるか検証して見ましょう。
光の座標P(x,y,z)=(c*cosθ,c*sinθ,0)を「ローレンツ変換」すると、P'(x',y',z')= {(ct*cosθ-vt)/√(1-v2/c2), ct*sinθ,0}となります。したがって
光の進んだ距離OP=√(x'2+y'2+z'2)= (c-v*cosθ)t/√(1-v2/c2) [m]
でした。一方、x=ct*cosθなので
光の進んだ時間t'=(t-vx/c2) /√(1-v2/c2)= (c-v*cosθ)t/c√(1-v2/c2)[s]
でした。故に
光の相対速度c'=√(x'2+y'2+z'2)= (c-v*cosθ)t/√(1-v2/c2) [m]÷(c-v*cosθ)t/c√(1-v2/c2)[s]=c[m/s]
となり、観測者Aと光の角度θにかかわらず、あらゆる方向の光の相対速度は「不変」となります。
しかし、物質を動かす電磁気力や重力は、ゲージ粒子である電磁波(光子)やグラビトン(重力子)が粒子間を往復することで生じます。現在では上記説明の様に、力は直線的に伝わるのではないことが分かっています。
また、様々な観測の結果「エーテル」は確認出来ませんでした。ですから、以上述べた思考方法は矛盾を含んでおり、弁証法による止揚(矛盾の解消)が必要でした。
６.光速度不変の原理の必要性
ではどうして、この様に摩訶不思議な「光速度不変の原理」が考案されたのでしょうか。
その理由は、v[m/s]で等速直線運動する(以下、「v慣性系」と言います)電磁石の強さが、同じv慣性系に居る観測者Aから見て、静止時と変わらなかったからです。
電磁気力は、電荷を帯びた粒子間を電磁波(光の一種)が、光速度cで往復して生じます。この2つの荷電粒子がvで移動しながら電磁波を交換すると、その電磁波の往復距離と往復時間は伸びます。ですから、常識では生じる電磁気力は弱まると思えます。
しかし実験の結果、それが変化しませんでした。そして、電磁気学の「マックスウェルの方程式」も、それは変化しないとしています。
そこで、アインシュタイン博士は「光速度不変の原理」を提唱されました。博士は、vで移動すると光の相対速度を不変とする様に、時間と空間が連動して「ローレンツ変換」すると思考されました。
v慣性系でも、2つの粒子から見て粒子間の距離は常にc[m]であり、電磁波の相対速度(粒子から離れて行く速度・粒子に近づいて来る速度)は行きも帰りも光速度cなので、静止時と同じ時間で電磁波は往復する。したがって観測者Aには、v慣性系でも電磁石の力は静止時と同じと観測される。
これで「エーテル」が不要となり、それが持っていた矛盾と、力はゲージ粒子の往復で伝わるのに力が直線的に片道で伝わるとした「ローレンツ理論」の矛盾は解消されました。
しかし、この「光速度不変の原理」も上記で説明したとおり
＞自分と並走する光を見ると自分の時間は遅れ空間は縮み、自分と対面する光を見ると自分の時間は速く進み空間は伸びます。では、併走する光と対面する光を同時に見たら、私に流れる時間や私の空間はどの様に変化するのでしょうか。また、どの光も見ずに目を瞑ったら時間や空間はどの様に変化するのでしょうか。更にこれでは、時間や空間は観測者の数だけ複数あることになります。つまり、観測者が新たに生まれたら、その人用の時間と空間が用意されるのです。＜
との深刻な矛盾を抱えています。
７.マイケルソンとモーレーの実験
この矛盾を解消する方法はあるのでしょうか。このHPでは、その未解決問題を探求します。
電磁石と観測者Aが、X軸正方向へv[m/s]で移動します。すると、粒子間を往復する電磁波の移動距離は、進行方向(以下、「横方向」と言います)では1/(1-v2/c2)倍、その上下左右方向(以下、「縦方向」と言います)では1/√(1-v2/c2)倍になります。
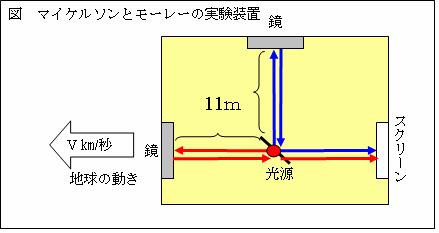この電磁波の往復距離の変化を、「マイケルソンとモーレーの実験」で説明します。
マイケルソンとモーレーは、地球が動くことにより観測者Aも動き、観測される光の速度が変化すると考えました。そして次の様な実験により、地球の進行方向から来る光の速度と、それ以外の方向から来る光の速度の差を確認しようとしました。
左図のとおり、光を片道11ｍの装置上を横方向（進行方向）と縦方向（上下方向）に、鏡を使い往復させました。
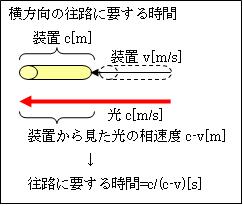
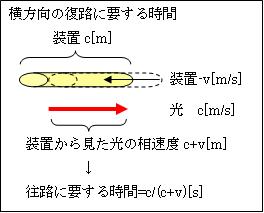計算の便宜上、横方向の片道を11[m]からc[m]に、縦方向の片道を11[m]から√(c2-v2)[m]に変更します。すると
光が横方向の往路に要する時間=c/(c-v)秒
光が横方向の復路に要する時間=c/(c+v)秒
光の横方向の往復時間=c/(c-v)+ c/(c+v)
= {c(c+v)+c(c-v)}/(c-v)(c+v)=(c2+cv+c2-cv)/(c2-v2)=2c2/(c2-v2)=2/(1-v2/c2)秒
光の横方向の往復距離={2/(1-v2/c2)}×c=2c/(1-v2/c2)[m]
です。静止時には光の往復距離は2c[m]なので、vで移動すると光の横の往復距離は、静止時の2c/(1-v2/c2)÷2c=1/(1-v2/c2)倍になります。
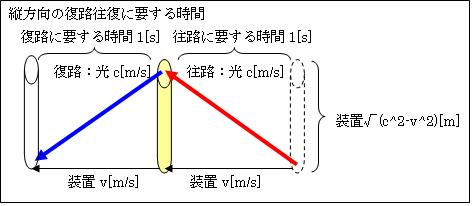次は、縦方向です。
光が縦方向の往路に要する時間=c÷c=1秒
光が縦方向の復路に要する時間=c÷c=1秒
光の往復時間=2秒
光の往復距離=2×c=2c[m]
静止時の光の往復時間=2√(c2-v2)÷c=2√(1-v2/c2)秒
静止時の光の往復距離=2√(1-v2/c2)×c=2c√(1-v2/c2)[m]
です。
したがって、vで移動すると光の縦の往復距離は、静止時の2c/√(1-v2/c2)÷2c=1/√(1-v2/c2)倍になります。
８.ローレンツ収縮
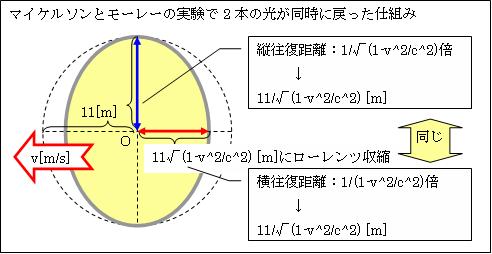以上のとおり、横往復すると光の移動距離は1/(1-v2/c2)倍になり、縦往復すると移動距離は1/√(1-v2/c2)倍になます。ですからマイケルソンとモーレーは、横往復した赤い光と縦往復した青い光は同時にはスクリーンに戻らず、スクリーン上に2本の光が干渉した縞模様が出来ると予測しました。
しかし実験結果は逆であり、MM装置をどちらに向けても、2本の光は同時に戻りました。
ローレンツはこの「矛盾」を解消する為に、v[m/s]で移動する物体は横方向へ√(1-v2/c2)倍「ローレンツ収縮」したと提唱しました。そうすると、光の往復距離は全ての方向で1/√(1-v2/c2)倍となり、左図のとおり11/√(1-v2/c2) [m]になるので、マイケルソンとモーレーの実験で2本の光は同時に戻ることが出来ます。
９.v慣性系の物体の運動の遅れ
では、電磁石の思考実験に戻ります。以上のとおりv慣性系では、電磁波の縦方向と横方向の往復時間は、1/√(1-v2/c2)倍になります。そして、生じる電磁気力の強さは、電磁波の1秒当たりの往復回数に比例します。故にv慣性系では、生じる電磁気力の強さは√(1-v2/c2)倍になります。
同様に、万有引力もグラビトンが粒子間を光速度cで往復して生じるので、v慣性系ではその強さは√(1-v2/c2)倍になります。
この様にv慣性系では、物体間に働く力の強さは√(1-v2/c2)倍になります。つまり、物体Oに同じ強さの力を加えたと思っても、Oにはその√(1-v2/c2)倍の力しか伝わりません。
「力F=ma (m=質量・a=加速度)」です。したがって、同じ力を加えても
v慣性系の力√(1-v2/c2)F=√(1-v2/c2)ma=ma'
v慣性系の加速度a'=√(1-v2/c2)a
となります。そして
「速度v=at (t=時間)」なので
v慣性系の物体Oの速度v'=√(1-v2/c2)at=√(1-v2/c2)v
です。
この様にv慣性系では、同じ力を加えても物体Oは静止系の√(1-v2/c2)倍の速度でしか動きません。これを相対性理論では
m=m0/√(1-v2/c2) (m=vで移動する物体の質量、m0=物体の静止時の質量)
と表します。実際に物体Oの質量が増えると、Oは増える前に比べてゆっくりと動きます。ですから、「高速で移動する物体Oは、まるでその質量が増加した様に振舞う」と言います。ただし、本当に物体Oの質量が増加したのではなくて、ただ動かし難くなっただけです。
１０.v慣性系の時計の遅れ
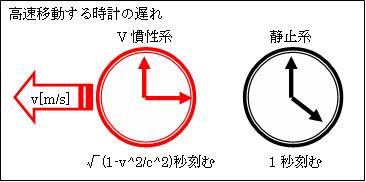この様に、v[m/s]で移動する時計を構成する粒子は、静止時の√(1-v2/c2)倍の速度でしか動きません。したがって、その時計は1秒間に√(1-v2/c2)秒時を刻みます。故に、時刻(時計で測定された時間)の変換式は
t'=t√(1-v2/c2)
です。同様にv[m/s]で移動する私も、ゆっくりと動き・思考し・年を取ります。ですから、私は自分の持っている時計が遅れたことに気が付きません。逆に、静止者Bの持っている時計が速く時を刻んで見えます。
この様にv慣性系では、同じ力を加えても静止系の√(1-v2/c2)倍の速度しか出ませんが、観測者Aの持つ時計が「t'=t√(1-v2/c2)」と遅れるので
Aから見た物体Oの速度v'=√(1-v2/c2)v÷√(1-v2/c2)=v[m/s]
と、Aには静止時と同じ速度で移動して見えます。
そして、光速度cに近づくにしたがって粒子が加速し難くなることは、加速器の実験で実証済みです。また、v[m/s]で移動する電子に同じ電磁気力Fを掛けても、電子は静止時の√(1-v2/c2)倍しか曲がらないことは、「カウフマンの実験」で証明されています。
また、v[m/s]で移動する原子核の周りを公転する電子も動き難くなり、それに掛かる遠心力は弱まります。すると、原子核の電磁気力に引かれて、電子はより小さい軌道上を公転します。この「理」により、v慣性系の物体Oは「ローレンツ収縮」します。
つまり私が持っている定規は、進行方向へ√(1-v2/c2)倍収縮します。私自身も同じ様に収縮するので、持っている定規が収縮したことに気が付きません。逆に、静止者Bの持っている定規が伸びて見えます。
１１.電磁波の往復時間は不変である
次に、命題「v慣性系の電磁波は、静止時と同じ時間で粒子αとβ間を往復する」ことを数式で証明します。
Ⅰ.半径c[m]の内面鏡
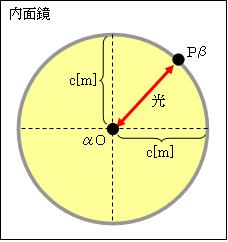ここで、半径c[m](c=光が1秒間に進む距離)の球体の内面鏡を設定します。その中心Oからあらゆる方向に光を発し、その光は球体の内面鏡に反射して中心Oに戻って来ます。中心Oに粒子αがあり、光が反射した球体の内面鏡上の任意の点Pに粒子βがあります。
光速度はc[m/s]なので、左図のとおり静止時Oから発した光は2秒でOに戻って来ます。
この内面鏡をv[m/s]で移動させ、粒子αから発した電磁波が粒子βに届き再び粒子αに戻って来るのに要する時間を計算します。
Ⅱ.内面鏡の座標の設定
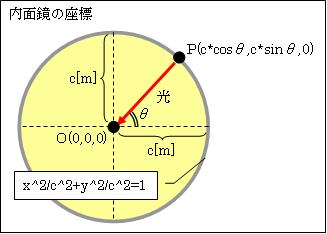次にこの内面鏡を、v[m/s]でX軸正方向へ移動します。すると、この内面鏡はX軸方向(横方向)へ√(1-v2/c2)倍「ローレンツ収縮」し、中心Oに居る観測者Aの持つ時計は「t'=t√(1-v2/c2)」と遅れます。
すると観測者Aは、中心Oからあらゆる方向へ発射された光が、内面鏡に反射して静止時と同じ2秒で中心Oに戻って来たと測定します。
そのことを、以下の方法で詳説します。
便宜上、光の座標を (x,y,z)=(ct*cosθ,ct*sinθ,0)と左図のとおり平面で表します。光は中心Oにある粒子αを発し、1秒後にPの位置にある粒子βに到達します。ですから粒子βの座標P=(c*cosθ,c*sinθ,0)です。光が移動した時間は1秒、光の移動した距離は√(x2,y2,z2)=√{(c*cosθ)2+(c*sinθ)2+02}=c[m]です。これを往路とします。
次に、粒子βに反射した光は、1秒後に中心Oに戻ります。これを復路とします。故に
静止系で光が往復した距離l=2c[m]
静止系で光の往復に要した時間t=2[s]
です。
Ⅲ.内面鏡のローレンツ収縮
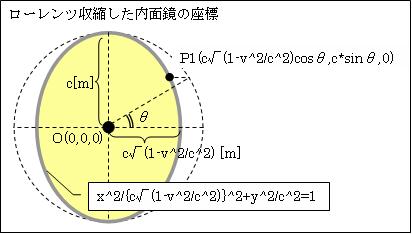次に速度vでX軸方向(横方向)に、この内面鏡を動かします。観測者Aも、この内面鏡と共に移動します。そしてOから光を発し、内面鏡に反射させて再びOに戻します。こうして、光の往復距離と往復時間を求めます。
この内面鏡の図形の方程式は、半径c[m]の円なので
①x2/c2+y2/c2=1
です。これが左図の点線の円です。
一方、vで移動するとこの内面鏡は、X軸方向へ√(1-v2/c2)倍「ローレンツ収縮」します。したがって、「ローレンツ収縮」した内面鏡の方程式は
②x2/{c√(1-v2/c2)}2+y2/c2=1
で、左図の灰色の楕円です。
Ⅳ.光の反射点を結んだ図形は楕円である
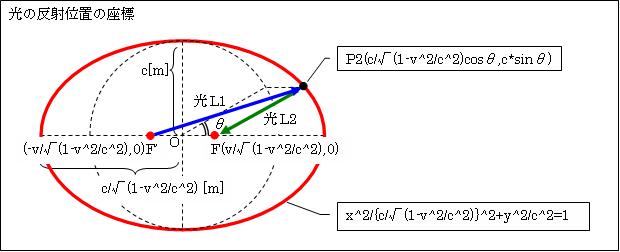この内面鏡をX軸の正方向へvで移動させつつ、中心Oからあらゆる方向へ光を発し、内面鏡に反射させ再び中心Oに戻します。すると、光が反射した点を結ぶと、円①をX軸方向へ1/√(1-v2/c2)倍引き伸ばした左図の赤色の楕円になります。
つまり、その図形の方程式は
③x2/{c/√(1-v2/c2)}2+y2/c2=1
です。
※以下の計算式で角度θが出てきますが、これらは全て元の円①の角度θです。楕円の円周上の点とOを結んだ直線とX軸との角度ではありません。ですから、同じθを②と③の楕円で使えます。このことに注意してください。
反射点を結んだ図形が楕円③になることを、数式を使って説明します。まず左図赤の楕円である図形③を使って、光の往路と復路の距離と時間を求めます。
この楕円③の、a= c/√(1-v2/c2)、b=cなので
離心率e=√(a2-b2)/a
です。
焦点F=(ae,0)=(√(a2-b2),0)=(v/√(1-v2/c2),0)
焦点F'=(-ae,0)=(-√(a2-b2),0)=(-v/√(1-v2/c2),0)
です。そして
光が反射した位置P2=(a*cosθ,b*sinθ)
です。光は焦点F'からP2に進みます。その時
光の往路の距離L1=√{( a*cosθ+ ae)2+(b*sinθ)2}
= √[{c* cosθ/√(1-v2/c2)}+ {v/√(1-v2/c2)}2+(c*sinθ)2]
= √[{(c* cosθ+v)/√(1-v2/c2)}2+(c*sinθ)2]
= √{(c* cosθ+v)2*(c2/c2-v2)+c2 sin2θ}
= √{(c2cos2θ+2cv *cosθ+v2)*(c2/c2-v2)+(c2sin2θ-v2 sin2θ) *(c2/c2-v2)}
= √{(c2/c2-v2) (c2cos2θ+2cv *cosθ+v2+c2sin2θ-v2 sin2θ) }
=√{(c2/c2-v2) (c2+2cv *cosθ+v2-v2(1- cos2θ) }
=√{(c2/c2-v2) (c2+2cv *cosθ+v2-v2+v2cos2θ) }
=√{(c2/c2-v2) (c2+2cv *cosθ+v2cos2θ) }
=√{(c2/c2-v2) (c+v*cosθ) 2}
=(c+v*cosθ)/√(1-v2/c2) [m]
です。
一方復路では、光はP2からFに進みます。その時
光の復路の距離L2=√{( a*cosθ- ae)2+(b*sinθ)2}
= √[{c* cosθ/√(1-v2/c2)} - {v/√(1-v2/c2)}2+(c*sinθ)2]
= √[{(c* cosθ-v)/√(1-v2/c2)}2+(c*sinθ)2]
= √{(c* cosθ-v)2*(c2/c2-v2)+c2 sin2θ}
= √{(c2cos2θ-2cv *cosθ+v2)*(c2/c2-v2)+(c2sin2θ-v2 sin2θ) *(c2/c2-v2)}
= √{(c2/c2-v2) (c2cos2θ-2cv *cosθ+v2+c2sin2θ-v2 sin2θ) }
=√{(c2/c2-v2) (c2-2cv *cosθ+v2-v2(1- cos2θ) }
=√{(c2/c2-v2) (c2-2cv *cosθ+v2-v2+v2cos2θ) }
=√{(c2/c2-v2) (c2-2cv *cosθ+v2cos2θ) }
=√{(c2/c2-v2) (c-v*cosθ) 2}
=(c-v*cosθ)/√(1-v2/c2) [m]
です。
光の速度=c[m/s]なので
往路に要する時間t1=(c+v*cosθ)/√(1-v2/c2)}÷c=(c+v*cosθ)/c√(1-v2/c2)[s]
復路に要する時間t2=(c-v*cosθ)/√(1-v2/c2)}÷c=(c-v*cosθ)/c√(1-v2/c2)[s]
です。したがって
光の往復距離l3=(c+v*cosθ)/√(1-v2/c2)}+ (c-v*cosθ)/√(1-v2/c2)}=2c/√(1-v2/c2)[m]
光の往復に要する時間t3=(c+v*cosθ)/c√(1-v2/c2)}+ 2c/√(1-v2/c2)=2/√(1-v2/c2)[s]
です。
Ⅴ.光の往路の距離
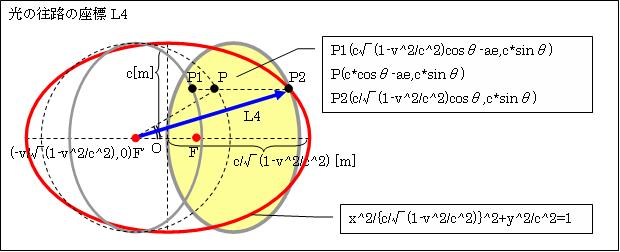次に、左図灰色の楕円であるローレンツ収縮した内面鏡②での説明に移ります。
この楕円②(左図の左側の灰色の楕円)は、a= c√(1-v2/c2)、b=cなので、円周上の任意の点P1=(a*cosθ,b*sinθ)={c√(1-v2/c2) cosθ,c*sinθ}です。
※この説明では、左の灰色の楕円の中心F'(赤の楕円の左側の焦点)を原点Oに取ります。
この楕円②(左の灰楕円)がX軸正方向へv[m/s]で移動します。そして上記のとおり、楕円③(左図赤の楕円)では、光の往路L4(F'P2)に要する時間は(c+v*cosθ)/c √(1-v2/c2)[s]でした。したがって、楕円②をその時間速度vで移動すると、楕円②の円周上の任意の点P1がP2の位置に来るか(楕円②が、黄色で塗りつぶした右の灰楕円の位置に来るか)を検証します。そうすると
楕円②の移動距離=v[m/s]×(c+v*cosθ)/c√(1-v2/c2)[s]=v(c+v*cosθ)/c√(1-v2/c2)[m]=P1P2
です。したがって
距離L4=√(P2のX座標の値2+P2のY座標の値2)
=√{(P1のX座標の値+P1P2)2+P2のY座標の値2}
=√[{c√(1-v2/c2) cosθ+v(c+v*cosθ)/c√(1-v2/c2)}2+ (c*sinθ)2]
=√[{√(c2-v2)cosθ+v(c+v*cosθ)/√(c2-v2)}2+c2sin2θ]
=√[{√(c2cosθ-v2 cosθ+cv+v2*cosθ)/√(c2-v2)}2+c2sin2θ]
=√[{c2(c*cosθ+v)2+c2(c2sin2θ-v2 sin2θ)}/(c2-v2)]
=√{c2cos2θ+2cv*cosθ+v2+c2sin2θ-v2 (1-cos2θ)}/√(1-v2/c2)
=√{c2 +2cv*cosθ+v2 -v2 +v2cos2θ)}/√(1-v2/c2)
=√{c2 +2cv*cosθ+v2cos2θ)}/√(1-v2/c2)
=√(c +v*cosθ)2/√(1-v2/c2)
=(c +v*cosθ)/√(1-v2/c2) [m]=L1
です。つまり、光が内面鏡の中心F'からP2に到着するのと、ローレンツ収縮した内面鏡上の任意の点P1がP2に到着するのが同時です。ですから光はP2の位置で反射し、その反射点を結ぶと赤色の楕円③になります。
Ⅵ.光の復路の距離
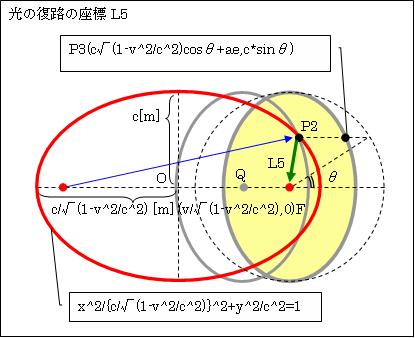そして、前記のとおり赤の楕円③で、緑で表した光の復路(P2F)の時間は、(c-v*cosθ)/c√(1-v2/c2)[s]でした。したがって、中心がQの位置にある灰色の楕円をその時間速度vで動かすと、その中心Qが赤い点で表した赤い楕円の焦点Fの位置に来るか(左の灰楕円②が黄色で塗つぶした右の楕円の位置に来るか)を検証します。
楕円②の移動距離=v[m/s]×(c-v*cosθ)/c√(1-v2/c2)[s]=v(c-v*cosθ)/c√(1-v2/c2)[m]=P3P2
です。
※便宜上この説明では、黄色で塗つぶした楕円の中心F(赤い楕円の右側の焦点)を原点Oに取ります(左図では、赤い楕円の長径と短径の交点を原点Oに取っています)。ですからP3={c√(1-v2/c2) cosθ,c*sinθ}です。
したがって
距離L5=√(P2のX座標の値2+P2のY座標の値2)
=√{(P3のX座標の値-P3P2)2+P2のY座標の値2}
=√[{c√(1-v2/c2) cosθ-v(c-v*cosθ)/c √(1-v2/c2)}2+ (c*sinθ)2]
=√[{√(c2-v2)cosθ-v(c-v*cosθ)/√(c2-v2)}2+c2sin2θ]
=√[{√(c2cosθ-v2 cosθ-cv+v2*cosθ)/√(c2-v2)}2+c2sin2θ]
=√[{c2(c*cosθ-v)2+c2(c2sin2θ-v2 sin2θ)}/(c2-v2)]
=√{c2cos2θ-2cv*cosθ+v2+c2sin2θ-v2 (1-cos2θ)}/√(1-v2/c2)
=√{c2 -2cv*cosθ+v2 -v2 +v2cos2θ)}/√(1-v2/c2)
=√{c2 -2cv*cosθ+v2cos2θ)}/√(1-v2/c2)
=√(c -v*cosθ)2/√(1-v2/c2)
=(c -v*cosθ)/√(1-v2/c2) [m]=L2
です。つまり、光がP2から内面鏡②の中心Fに到着するのと、ローレンツ収縮した内面鏡の中心がQからFに到着するのが同時です。ですから赤の楕円③の円周上の点P2で反射した光は、赤色の楕円③の焦点Fに戻ります。
Ⅶ.まとめ
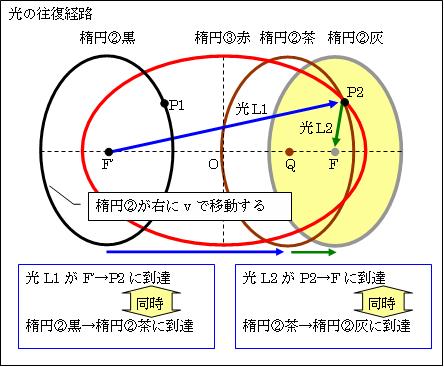以上のとおりL1=L4、L2=L5となります。
即ち、楕円②黒のP1が楕円②茶のP2に到着するのと、楕円③赤の左の焦点F'(楕円②黒の中心)から発した光が楕円③の円周上の任意の点P2に到着するのとが同時です。故に、vで移動する楕円②の中心から発した光の反射点を結ぶと、楕円③になります。
そして、P2を発した光が楕円③赤の右の焦点Fに戻るのと、楕円②茶の中心Qが楕円②灰の中心Fに到達するのとが同時です。
つまり、内面鏡が「ローレンツ収縮」しながらvで進むと、光の反射点は楕円③赤となります。光は楕円③赤の一方の焦点F'から発し、その楕円③赤の円周上の任意の点P2で反射し、楕円③赤のもう一方の焦点Fに戻ります。
この様に内面鏡は、逆にX軸方向へ1/√(1-v2/c2)倍伸びて見えます。
Ⅷ.v慣性系では電磁波の往復距離と往復時間は1/√(1-v2/c2)倍となる
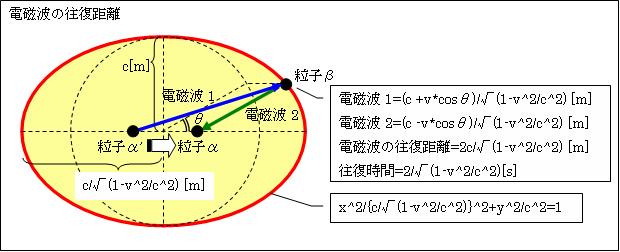以上のとおりv慣性系では、左図の楕円赤③の焦点F'から発した電磁波は、円周上の任意の点P2で反射し、もう一方の焦点Fに戻ります。F'-P2-Fの長さは、楕円赤③の長径c/√(1-v2/c2)[m]の2倍です。つまりv慣性系の全ての方向で
光の往復距離L'=2c/√(1-v2/c2)[m]
光の往復に要した時間t'=2/√(1-v2/c2)[s]
と、「1/√(1-v2/c2)倍」になります。
Ⅸ.v慣性系の時計は√(1-v2/c2)倍遅れるので往復では光速度不変となる
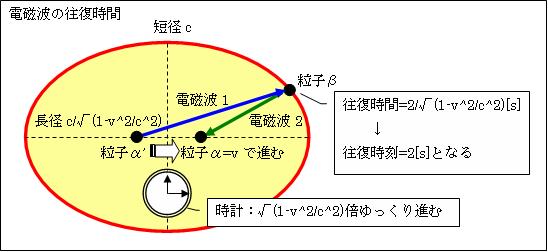そしてvで移動する観測者Aが持つ時計は、「t'=t√(1-v2/c2)」と遅れるので
Aから見た光の往復時間={2/√(1-v2/c2)}×√(1-v2/c2)=2[s]
です。
このとおり電磁波は、v慣性系でも静止系と同じ2秒で荷電粒子間を往復します。つまり、光の往復での平均速度は、必ず光速度cになります。
したがって、Aには電磁石の強さが不変と観測されます。これを｢特殊相対性原理｣と言います。
１２.ローレンツ変換登場
この様に、静止時の光の片道の移動距離はc[m]ですが、内面鏡がローレンツ収縮してvで移動すると
光の往路の移動距離=(c+v*cosθ)/√(1-v2/c2) [m]・・・(1)
光の復路の移動距離=(c -v*cosθ)/√(1-v2/c2) [m]・・・(2)
となります。
これを(x,y,z)で表わすと、復路は
①x'= (x-vt)/√(1-v2/c2)
②y'=y
③z'=z
です。このことを説明します。
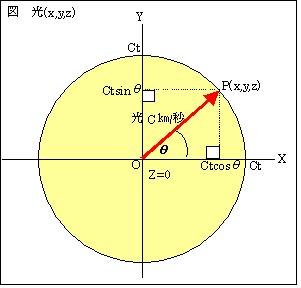光の座標P=(x,y,z)=(ct*cosθ,ct*sinθ,0)なので、これを①②③を使って変換すると、P' (x',y',z')={(ct*cosθ-vt)/√(1-v2/c2), ct*sinθ,0}となります。したがって
復路P'Oの長さ= √[{(ct* cosθ-vt)/√(1-v2/c2)} 2+(ct*sinθ)2]
= t√{(c* cosθ-v)2*(c2/c2-v2)+c2 sin2θ}
= t√{(c2cos2θ-2cv*cosθ+v2)*(c2/c2-v2)+(c2*sin2θ-v2 sin2θ) *(c2/c2-v2)}
= t√{(c2/c2-v2) (c2cos2θ-2cv*cosθ+v2+c2sin2θ-v2 sin2θ) }
=t√{(c2/c2-v2) (c2-2cv *cosθ+v2-v2(1- cos2θ) }
=t√{(c2/c2-v2) (c2-2cv *cosθ+v2-v2+v2cos2θ) }
=t√{(c2/c2-v2) (c2-2cv *cosθ+v2cos2θ) }
=t√{(c2/c2-v2) (c-v*cosθ) 2}
=(c-v*cosθ)t/√(1-v2/c2) [m]
です。t=1[s]を代入すると
復路P2Fの長さ=(c-v*cosθ)/√(1-v2/c2) [m]
です。これで(2)が導けました。
ところで、復路の光と観測者Aとの進行方向の角度=θなので、往路ではその角度=(π-θ)です。cos(π-θ)=-cosθなので
往路F'P2の長さ=√(x'2+y'2+z'2)= (c+vcosθ)t/√(1-v2/c2)[m]
です。t=1[s]を代入すると
往路F'P2の長さ=(c+v*cosθ)/√(1-v2/c2) [m]
です。これで(1)が導けました。
そして、光の速度=cなので
光が復路に要する時間=(c-v*cosθ)t/c√(1-v2/c2)
光が往路に要する時間=(c+v*cosθ)t/c√(1-v2/c2)
です。したがって、復路の時間は
④t'=(c-v*cosθ)t/c√(1-v2/c2)
となります。光のX軸の座標x=ct*cosθなので、cosθ=x/ctです。これを④に代入すると
④t'=(c-v*cosθ)t/c√(1-v2/c2)= (c-vx/ct)t/c√(1-v2/c2)=(t-vx/c2) /√(1-v2/c2)
です。まとめると、復路では
①x'=(x-vt)/√(1-v2/c2)
②y'=y
③z'=z
④t'=(t-vx/c2) /√(1-v2/c2）
と「ローレンツ変換」になります。
一方往路では、xの値はct*cos(π-θ)=-ct*cosθ、vは-vとなるので
①x'=(-x+vt)/√(1-v2/c2)= -(x-vt)/√(1-v2/c2)
②y'=y
③z'=z
④t'=(t-vx/c2) /√（1-v2/c2）
です。この様に往路では、光の進む方向が復路とは逆になる(xがマイナスになる)ので、やはり「ローレンツ変換」になります。
このとおり、静止者Bがv慣性系にある時計を見ると
光の往復に要する時間t'={(c-v*cosθ)t/√(1-v2/c2)+ (c+vcosθ)t/√(1-v2/c2)}÷c=2t/√(1-v2/c2)= 2t√(1-v2/c2)/√(1-v2/c2)=2t[s]
となります。v慣性系でも電磁波は、静止時と同じ時間で粒子間を往復して見えるので、静止者Bにはv慣性系の電磁石の強さは不変と観測されます。
１３.v慣性系の座標に変換する方法
Ⅰ.静止者Bが見た値
以上のとおり、荷電粒子がvで移動しながら電磁波を交換すると、その電磁波の移動距離と移動時間は、静止時の値が「ローレンツ変換」されたものとなります。
ただし、これは静止者Bが見た「距離」と「時間」です。これをvで移動する観測者Aが見たら、一体幾らと測定するでしょうか。Bが見た光の座標を(x,y,z)、Aが見た光の座標を(x',y',z')とします。
Ⅱ.観測者Aの時計の遅れ
前述のとおり、観測者Aの持つ時計は1秒間に√(1-v2/c2)秒刻みます。
ですから、静止系の値tをv慣性系の値t'に変換するには
④t'=t√(1-v2/c2)
です。
Ⅲ.観測者Aの定規の変化
そして便宜上、静止時の定規の長さをc[m]とします。この定規が「ローレンツ収縮」した状態で速度vで進みます。つまりこの定規の両端は、常に上記球体の内面鏡の中心と円周上の任意の点にあります。ですから、光はこの定規の一方の端から他方の端まで進みます。その長さは「ローレンツ変換」されるので、⑪(c-v*cosθ)/√(1-v2/c2) [m]になります。
v慣性系ではこの定規を使うので、⑪の光の移動した長さを元のc[m]と測定します。つまり、静止系からv慣性系への変換式は「ローレンツ変換」の逆変換です。したがって
①x'=x√(1-v2/c2)+vt
②y'=y
③z'=z
です。
Ⅳ.横方向の空間の変換式の説明
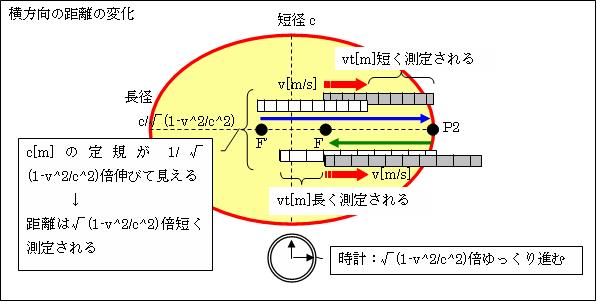そのことを、X軸方向とY軸方向に分けて説明します。
定規は「ローレンツ収縮」しながらvで進むので、その両端は逆に1/√(1-v2/c2)倍に伸びて見えます。つまり、半径c[m]の円は、左図の赤の楕円の様に、横に1/√(1-v2/c2)倍伸びて見えます。ですからこの定規を使うと、距離は√(1-v2/c2)倍短く測定されます。
そして復路では、左図の緑光が定規の端P2から右の焦点Fまで進む間に、定規は光が出発した方向へvt/√(1-v2/c2)[m]進むので、定規の目盛にして{vt/√(1-v2/c2)}×√(1-v2/c2)=vt[m]長く測定されます。ですから観測者Aは、静止系の距離x[m]を√(1-v2/c2)倍してvt[m]足した長さに測ります。つまり
①x'=x√(1-v2/c2)+vt
です。
一方往路では、左図の青光が定規の端Fから端P2に進む間に、定規は光が進む方向へvt/√(1-v2/c2)[m]進むので、定規の目盛にして{vt/√(1-v2/c2)}×√(1-v2/c2)=vt[m]短く測定されます。ですから観測者Aは、静止系の距離x[m]を√(1-v2/c2)倍してvt[m]引いた長さに測ります。つまり
①x'=x√(1-v2/c2)-vt
です。往路ではvが-vなので、往路と復路で変換式は同じです。
Ⅴ.縦方向の空間の変換式の説明
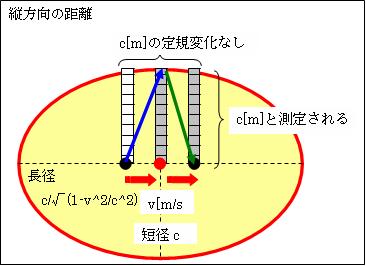
これに対して、縦方向では左図のとおり変化はありません。
Ⅵ.有木変換とCATBIRD変換
まとめると、静止系からv慣性系への時間と空間の変換式は
①x'=x√(1-v2/c2)+vt
②y'=y
③z'=z
④t'=t√(1-v2/c2)
です。これを「有木変換」と言います(2020/07/22pm14:31)。更に、これを
⑤x=(x'-vt)/√(1-v2/c2)
⑥y=y'
⑦z=z'
⑧t=t'/√(1-v2/c2)
と変形したものを「CATBIRD変換」と言います。(2020/07/22pm14:31)
つまり、「有木変換」は静止系の時間と空間をv慣性系の値に変換し、「CATBIRD変換」はv慣性系の時間と空間を静止系の値に変換します。
ところで、森羅万象は「有」の振動で表され計算されます。ですから、光は「有」の中を振動として伝わります。そして、この「有」が運動の基準となる「相対的静止系」です。v[m/s]で移動する内面鏡の中心から発した光が、内面鏡に到達するまでに
光が進んだ距離L1=√(x'2+y'2+z'2)= (c-v*cosθ)/√(1-v2/c2)[m]
光が進んだ時間t1=(c-v*cosθ)/c√(1-v2/c2)[s]
でした。ですから
相対的静止系に居る静止者Bが見た光の速度= (c-v*cosθ)/√(1-v2/c2)[m]÷(c-v*cosθ)/c√(1-v2/c2)[s]=c[m/s]
です。
一方、v慣性系に居る観測者Aは、時間と空間の座標が「有木変換」するので、L1=c[m]、t1=(c-v*cosθ)/c[s]と測定します。したがって
観測者Aが見た光の相対速度c'= c[m]÷(c-v*cosθ)/c[s]=c2/(c-v*cosθ)[m/s]
です。
Ⅶ.リングレーザージャイロへのプログラム
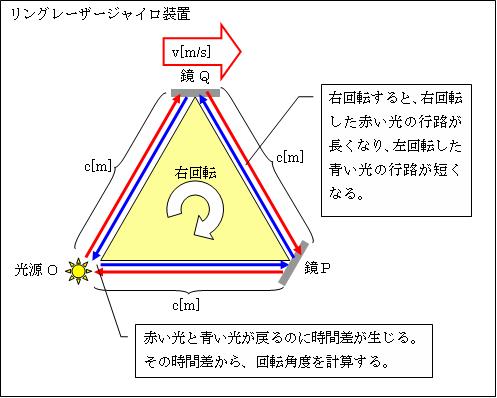ところで、ロケットの方向の変化を測定する「リングレーザージャイロ装置」には
光が進んだ距離L= (c-v*cosθ)[m]
光が進んだ時間t=(c-v*cosθ)/c[s]
とプログラムされています。これはどうしてでしょうか。
まず、「リングレーザージャイロ装置」の仕組みを説明します。この装置では、正三角形の２つの頂点にPQ２枚の鏡を置き、光源Oから発した光を反射させて正三角形に右回りと左回りに回らせます。そして、右回りした赤い光と左回りした青い光とのOへの到着時刻の時間差より、ロケットの回転角度を計算します。
説明の便宜上、三角形の一辺をc[m]とします。装置がvで移動すると、「ローレンツ変換」され
光が三角形の一辺の行路を進んだ距離L1=√(x'2+y'2+z'2)= (c-vcosθ)/√(1-v2/c2)[m]
光がそれに要した時間t1=(c-v*cosθ)/c√(1-v2/c2)[s]
でした。
しかし、ロケットに搭載した時計は「t'=t√(1-v2/c2)」と遅れるので
ロケット搭載の時計で計った光が進んだ時間t2=(c-v*cosθ)/c√(1-v2/c2)×√(1-v2/c2)= (c-v*cosθ)/c[s]
です。
そこで、この装置の設計者は、赤と青の光の相対速度をあくまでもc[m/s]とし、光はロケット搭載の時計で(c-v*cosθ)/c[s]進んだので
装置から見た光が三角形の一辺の行路を進んだ距離L2= (c-v*cosθ)/c[s]×c[m/s]= (c-v*cosθ)[m]
として計算するよう、この装置にプログラムします。
すると
左周りした青い光の行路の距離L3=OP+PQ+QO=(c-v*cos0°)+ (c-v*cos120°)+ (c-v*cos240°)= (c-v*cos0°)+ (c+v*cos60°)+ (c+v*cos60°)= (c-v)+ {c+(1/2)v}+ {c+(1/2)v}=3c[m]
左周りした青い光が一周するのに要した時間t3=(c-v*cos0°)/c+ (c-v*cos120°)/c+ (c-v*cos240°)/c= (c-v*cos0°)/c+ (c+v*cos60°)/c+ (c+v*cos60°)/c= (c-v)/c+ {c+(1/2)v}/c+ {c+(1/2)v}/c=3[s]
です。
また
右周りした赤い光の行路の距離L4=OQ+QP+PO=(c-v*cos60°)+ (c-v*cos300°)+ (c-v*cos180°)= (c-v*cos60°)+ (c-v*cos60°)+ (c+v*cos0°)= {c-(1/2)v}+ { c-(1/2)v }+ {c+v}=3c[m]
右周りした赤い光が一周するのに要した時間t4=(c-v*cos60°)/c+ (c-v*cos300°)/c+ (c-v*cos180°)/c= (c-v*cos60°)/c+ (c-v*cos60°)/c+ (c+v*cos0°)/c= {c-(1/2)v}/c+ { c-(1/2)v }/c+ {c+v}/c=3[s]
です。
この様に装置が回転しなければ、左回りした青い光も、右回りした赤い光も、3c[m]の行路をc[m/s]で進んで3[s]でOに戻って来たと計算できます。
そして装置が右に回転すると、右回りした赤い光の行路が伸び、左回りした青い光の行路が短くなります。その為に、青い光は赤い光よりも早くOに戻ります。その時間差を計り、ロケットの回転角度を計算します。
このとおり「リングレーザージャイロ装置」は、特殊相対論効果を利用して作られています。
Ⅷ.有木変換から光行差のブラッドリーの式を導く
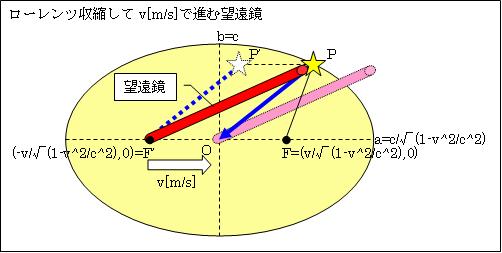速度v[m/s]で移動する地上で、望遠鏡を使って星Pを見ます。説明の便宜上、望遠鏡の長さをc[m]とします。
F'の位置で観測者Aは、赤い筒で表した望遠鏡を覗いています。Aと望遠鏡はF'からOへ、v[m/s]で移動します。星Pは遥か遠方にあるので、F'の位置ではF'-P'が星の在る方向です。一方星Pから発した光は、P-Oと進みます。ですからAは、望遠鏡をF'-Pと少し前に傾けてやらなければなりません。そうすると、Pを通った星から来た光は、P-Oと上手に望遠鏡の筒の中を通り抜け、観測者Aの目に届きます。
v[m/s]で移動すると、前記のとおり、半径c[m]の円形の内面鏡は進行方向へ1/√(1-v2/c2)倍伸びた楕円形となります。つまり、望遠鏡もそれに合わせて図のとおり、進行方向へ1/√(1-v2/c2)倍伸びた形になります。
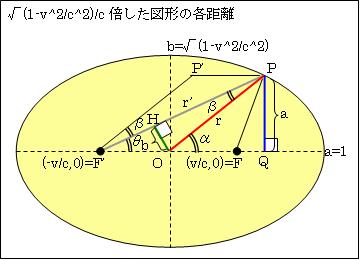説明の便宜上、図を√(1-v2/c2)/c倍縮小します。全体を均等に収縮するので、角度は同じです。本来星の在る角度∠P'F'O=∠POF=α、望遠鏡の角度∠PF'O=θ、α-θ=βとします。すると
sinβ=(v/c)sinα
と表せます。これを「ブラッドリーの式」と言います。
この導き方を説明します。OP=r、F'P=r'とします。したがって
sinα=a/r、sinβ=b/rです。∴sinβ=(b/a) sinαです。そして
a=r'sinθ、b=(v/c)sinθ
です。故に
(b/a)= (v/c)sinθ÷r'sinθ=(v/c)(1/r')
です。したがって
sinβ=(v/c)(1/r') sinα
です。
縮小する前の図に戻ります。F'を原点に取ると、P={c*cosθ/√(1-v2/c2)+v/√(1-v2/c2),c*sinθ}です。これを「有木変換」してv慣性系の数値に変換します。t=1[s]として往路の「有木変換」すると
①x'=x√(1-v2/c2)-vt={c*cosθ/√(1-v2/c2)+v/√(1-v2/c2)} √(1-v2/c2)+v=c*cosθ
②y'=y=c*sinθ
③z'=z=0
です。したがって
v慣性系の観測者Aが測るr'の長さ=√{(c*cosθ)2+( c*sinθ)2}=c[m]
です。一方
F'O=v/√(1-v2/c2)
です。∴
観測者AがF'→Oに移動するのに要する時間= v/√(1-v2/c2)÷v=1/√(1-v2/c2)秒
です。しかし、時間も「有木変換」するので
④t'=t√(1-v2/c2)= 1/√(1-v2/c2)×√(1-v2/c2)=1[s]
と観測者Aは測定します。したがって
観測者Aが測るF'Oの長さ=v[m/s]×1[s]=v[m]
です。
そうすると
a=r'sinθ=c*sinθ、b=v*sinθ
なので
(b/a)=v*sinθ÷c*sinθ=(v/c)
です。故に
sinβ=(v/c) sinα
となり、「有木変換」より「ブラッドリーの式」が導かれます。
言葉を変えて再度説明します。
以上のとおり、観測者Aから見ると時間と空間の座標が「有木変換」するので、F'P=c[m]、F'O=v[m]と測れます。そのために
OP=√(c2+v2-2cv*cosθ)
となります。故に
sinα=c*sinθ/√(c2+v2-2cv*cosθ)
cosα=(c*cosθ-v)/ √(c2+v2-2cv*cosθ)
です。すると
sinβ=sin(α-θ)=sinα*cosθ-cosα*sinθ (公式より)
= {c*sinθ/√(c2+v2-2cv*cosθ)} cosθ-{(c*cosθ-v)/ √(c2+v2-2cv*cosθ)}sinθ
= {sinθ/√(c2+v2-2cv*cosθ)}(c* cosθ-c*cosθ+v)=v*sinθ/√(c2+v2-2cv*cosθ)
=(v/c)sinα
と、「ブラッドリーの式」が導かれます。
Ⅸ..v慣性系の光の往復平均速度は常にcとなる
内面鏡がvで移動すると、光の座標は(x,y,z,t)から{(x-vt)/√(1-v2/c2),y,z,(t-vx/c2)/√(1-v2/c2)}にローレンツ変換され伸びます。それをv慣性系の観測者Aは、「ローレンツ収縮して移動する定規」と「遅れた時計」を使うので、その値は「有木変換」され
①x'={(x-vt)/√(1-v2/c2)}√(1-v2/c2)+vt=x
②y'=y
③z'=z
④t'={(t-vx/c2) /√(1-v2/c2)}√(1-v2/c2)= t-vx/c2
と測定します。
そして
光の移動距離=√(x'2+y'2+z'2)= √(x2+y2+z2)=√{(ct*cosθ)2+(ct*sinθ)2+02}=ct
です。x=ct*cosθなので
光の速度c'=ct/(t-vx/c2)=ct/(t-vct*cosθ/c2)=c2/(c-v*cosθ)
です。
したがって
Aから見た光の復路時間=√(x2+y2+z2)÷c2/(c-v*cosθ)=ct×(c-v*cosθ) /c2=(c-v*cosθ)t/c
Aから見た光の往路時間=√(x2+y2+z2)÷c2/(c+v*cosθ)=ct×(c+v*cosθ) /c2=(c+v*cosθ)t/c
Aから見た光の往復時間={(c-v*cosθ)t /c}+{(c+v*cosθ)t/c}=2t[s]
です。
つまりvで移動する観測者Aは、電磁波が粒子間を静止時と同じ時間で往復すると計ります。ですからAには、電磁石の強さは静止系と同じで不変と見えます。
ⅹ.矛盾の解消
これで、＞自分と並走する光を見ると自分の時間は遅れ空間は縮み、自分と対面する光を見ると自分の時間は速く進み空間は伸びます。では、併走する光と対面する光を同時に見たら、私に流れる時間や私の空間はどの様に変化するのでしょうか。また、どの光も見ずに目を瞑ったら時間や空間はどの様に変化するのでしょうか。更にこれでは、時間や空間は観測者の数だけ複数あることになります。つまり、観測者が新たに生まれたら、その人用の時間と空間が用意されるのです。＜
との深刻な矛盾は解消されました。
「有木変換」で静止系の時間をv慣性系の時間に直す際、自分の進む方向と光の進む方向との角度θは出てきません。つまり、どの方向へ進む光を見ても何も見なくても、変換後の時間は「④t'=t√(1-v2/c2)」と同じ値です。そして、時計が遅れる仕組みは前述のとおりです。
また、空間自体が変化するのではなくて、定規の長さが変化します。私が移動する方向と定規との角度θにより、定規の長さが異なる仕組みも前述のとおりです。
そして、光の相対速度はc2/(c-v*cosθ)[m/s]であり、自分の進む方向と光の進む方向との角度θにより、常識のとおり光の相対速度c'は変わります。更に、時間と空間は1つです。時間と空間の座標が変化するのは、各人が持っている時計や定規が変化するからです。
これで、理性が悲鳴を上げることはありません。
１４.光速度不変の要請
それならどうして、摩訶不思議な片道での「光速度不変の原理」が提唱されたのでしょうか。
「有木変換」では、あらゆる方向へ進む電磁波の往路と復路を別々に計算しなければなりません。しかし、それは事実上不可能です。
そこで物理計算を可能にするために、片道でも「光速度不変」と仮設しました。生じる電磁気力の強さは、1秒間当たりの電磁波の往復回数に比例するので、その様に仮設して計算しても何ら不都合はありません。
１５.ローレンツ変換の逆変換
片道でも「光速度不変」にするには、静止者Bから見た光の移動時間「(t-vx/c2) /√(1-v2/c2)[s]」が、観測者Aから見てt[s]と見える様に、変換式を調整する必要があります。つまり、ローレンツ時間変換「t'=(t-vx/c2) /√(1-v2/c2)」の逆変換をしなければなりません。すると
⑨t'=t√(1-v2/c2)+vx/c2
となります。⑨式のtに「(t-vx/c2) /√(1-v2/c2)」を代入すると
⑨t'={(t-vx/c2) /√(1-v2/c2)}√(1-v2/c2)+vx/c2=t
となります。また、
①x'={(x-vt)/√(1-v2/c2)}√(1-v2/c2)+vt=x
②y'=y
③z'=z
でした。まとめると
①x'=x
②y'=y
③z'=z
⑨t'=t
となります。①②③⑨のとおり、あらゆる慣性系で同じ物理現象を観測しても、得られる時間の値と空間の値は同じになるので、あらゆる慣性系で物理法則は同じ形となります。
この様に、静止系の時空間の値をv慣性系の数値に直すには、下記のとおり、「ローレンツ変換」の逆変換をします。
⑤x'=x√(1-v2/c2)+vt
⑥y'=y
⑦z'=z
⑨t'=t√(1-v2/c2)+vx/c2
１６.ローレンツ変換そのもので逆変換できるケース
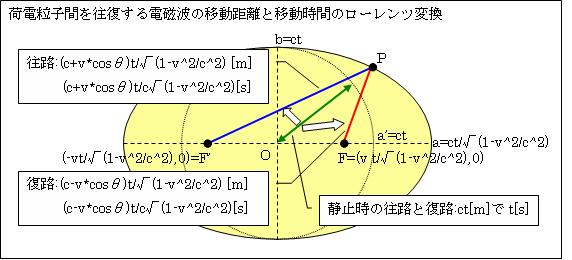しかし、「ローレンツ変換」そのもので、v慣性系の観測者Aの測定値に逆変換できるケースがあります。そのことを説明します。
今までの説明のとおり、c[m]離れた2つの荷電粒子が、v[m/s]で移動しながら電磁波を交換すると、電磁波の移動距離Lと移動時間tは「ローレンツ変換」されます。つまり
①x'=(x-vt)/√(1-v2/c2)
②y'=y
③z'=z
④t'=(t-vx/c2) /√(1-v2/c2）
です。これは「復路」であり、「往路」は-v→+vです。
この時、光の進む距離L'=√(x'2+y'2+z'2)、x=ct*cosθなので、既に説明したとおり
静止者Bから見た電磁波の進む距離PF(赤い光)L'=(c-v*cosθ)t/√(1-v2/c2) [m]・・・(1)
静止者Bから見た電磁波の進む時間t'=(c-v*cosθ)t/c√(1-v2/c2) [s] ・・・・・・・(2)
です。
また、静止時は緑の光のとおり
電磁波の進む距離L=ct[m]
電磁波の進む時間t=t[s]
で往復します。したがって
静止者Bから見た電磁波の進む距離L'=(L-vt*cosθ)/√(1-v2/c2) [m] ・・・(3)
静止者Bから見た電磁波の進む時間t'=(L-vt*cosθ)/c√(1-v2/c2) [s]・・・(4)
です。これが「ローレンツ変換」です。
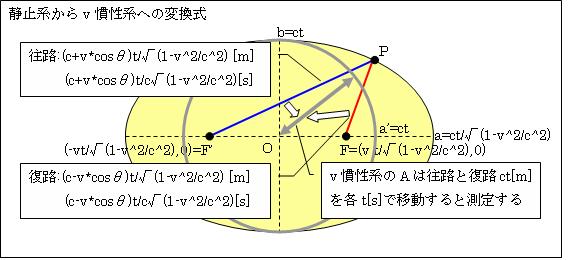v慣性系において片道でも「光速度不変」と仮設すると、青の往路も赤の復路も灰色の矢印のとおり、L'=ct[m]、t'=t[s]と測定します。ですから、v慣性系に居るAの測定値を求めるには、距離L'と時間t'を「ローレンツ変換」の逆変換をします。それは
⑤x'=x√(1-v2/c2)+vt
⑥y'=y
⑦z'=z
⑧t'=t√(1-v2/c2)+vx/c2
です。つまり
v慣性系に居る観測者Aから見た電磁波の進む距離L2=L'√(1-v2/c2)+vt*cosθ ・・・・・(5)
v慣性系に居る観測者Aから見た電磁波の進む距離t2=ct'√(1-v2/c2)/ (c-v*cosθ)・・・(6)
です。これで(3)(5)より
L2=L'√(1-v2/c2)+vt*cosθ={(L-vt*cosθ)/√(1-v2/c2)} ×√(1-v2/c2)+vt*cosθ=L=ct[m]
(2)(6)より
t2=ct'√(1-v2/c2)/ (c-v*cosθ)= {(c-v*cosθ)t/c√(1-v2/c2)}×c√(1-v2/c2)/ (c-v*cosθ)=t[s]
と、v慣性系に居るAの測定値になります。観測者Aは、黄色い楕円を灰色の円と観測します。
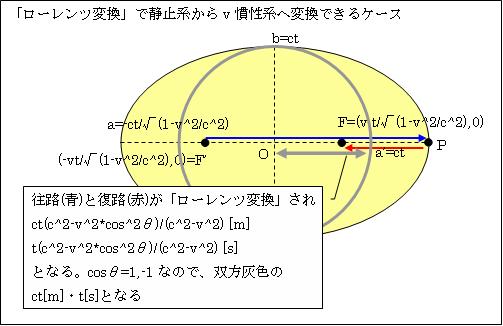しかし摩訶不思議なことに、「ローレンツ変換」された電磁波の青の往路と赤の復路を、「ローレンツ変換」そのもので逆変換してv慣性系のAの測定値にできるケースがあるのです。「ローレンツ変換」のvを-vにし、(x',y',z')と(x,y,z)を入れ替えると、逆変換できます。つまり
⑨x=(x'+vt')/√(1-v2/c2)
⑩y=y'
⑪z=z'
⑫t=(t'+vx'/c2) /√(1-v2/c2）
です。∴
v慣性系に居る観測者Aから見た電磁波の進む距離L2=(L'+vt'*cosθ)/√(1-v2/c2) [m] ・・・(7)
v慣性系に居る観測者Aから見た電磁波の進む距離t2=(L'+vt'*cosθ)/c√(1-v2/c2) [s]・・・(8)
です。⑨⑩⑪⑫と(7)(8)を「ローレンツ逆変換」と言います。
では、それを計算して行きます。
L2=(L'+vt'*cosθ)/√(1-v2/c2) ={(L-vt*cosθ)/√(1-v2/c2)+v*cosθ(L-vt*cosθ)/c√(1-v2/c2)}/√(1-v2/c2)
={(ct-vt*cosθ)/√(1-v2/c2)+v*cosθ(ct-vt*cosθ)/c√(1-v2/c2)}/√(1-v2/c2)
=(c2t-cvt*cosθ+cvt*cosθ-v2t*cos2θ)/c(1-v2/c2)
=(c2t-v2t*cos2θ)/{(c2-v2)/c}
=ct(c2-v2*cos2θ)/(c2-v2)
です。
同様に
t2=(L'+vt'*cosθ)/c√(1-v2/c2) ={(L-vt*cosθ)/√(1-v2/c2)+v*cosθ(L-vt*cosθ)/c√(1-v2/c2)}/c√(1-v2/c2)
={(ct-vt*cosθ)/√(1-v2/c2)+v*cosθ(ct-vt*cosθ)/c√(1-v2/c2)}/c√(1-v2/c2)
=(c2t-cvt*cosθ+cvt*cosθ-v2t*cos2θ)/c2(1-v2/c2)
=(c2t-v2t*cos2θ)/(c2-v2)
=t(c2-v2*cos2θ)/(c2-v2)
です。
そして「cosθ=1,-1」の時、つまり観測者Aが光と対面する形で進む時「θ=0°」、観測者Aと光が並走する時「θ=180°」のケースでは
L2=ct(c2-v2*cos2θ)/(c2-v2) =ct(c2-v2)/(c2-v2)=ct[m]
t2=t(c2-v2*cos2θ)/(c2-v2) =t(c2-v2)/(c2-v2)=t[s]
と、v慣性系のAの観測値ct[m]・t[s]となります。
これ以外の時、即ちθ≠0°やθ≠180°のケースでは、「ローレンツ逆変換」しても、v慣性系の測定値ct[m]・t[s]にはなりません。
しかし「ローレンツ変換」は、この特定のケースで「ローレンツ変換」そのものを使って逆変換出来ると言う不思議な性質を持つので、「静止系がない」とする思考様式に適していました。つまり静止系がなければ、「ローレンツ変換」のみで、相互の系の観測者の測定値に、変換と逆変換できなければならないからです。
ただし現在では、光も物質も宇宙時空間に充満する「有」の振動と考えられており、これが運動の基準となる「相対的静止系」です。ですから、θ≠0°やθ≠180°のケースでは、「ローレンツ変換」の逆変換をすればOKです。
これでv慣性系では、片道でも「光速度不変」となり、静止系の物理方程式をそのまま使うことが出来ます。更に、逆変換も同じ方程式で行えます。この様に、「光速度不変の原理」は物理計算を可能にした「偉大な発明」です。
片道で「光速度不変」とすると、前述した深刻な矛盾が生じ、我々の理性は悲鳴を上げます。しかし、その様に仮設して物理計算しても無矛盾であり、逆にその様に仮設しないと物理計算は不可能です。
１７.運動の基準となる系
そして光も物質も、「有」の振動です。そして、「有」の振動は光速度cで伝わります。そのために光は、「有」を光速度cで伝わります。一方物質は、「有」を伝わると質量を獲得し動き難さを与えられるので、光速度c未満でしか移動出来ません。
ですから、この「有」が物体Oの運動の基準となる「相対的静止系」です。物体Oが「有」に対して動くと質量を与えられ、「有」に対して加速するとGが掛り、「有」に対して回転すると遠心力が掛かります。
しかし、この「有」は相対性理論が否定する「絶対静止系」ではありません。空間自体に「絶対静止の一点」の印を付けることが出来ないからです。ここが静止していると指差していても、その指自体が動いているかも知れません。ですから、「有」が空間の中でどの様に移動しているのか誰にも分からないので、その「有」は「相対的静止系」です。
しかし質量もGも遠心力も、「有」に対する相対的運動により生じます。そして｢有｣には、「静止の一点」を付けることが出来ます。ですから、物体Oの「有」に対する相対的運動を計算することが必要でそれで十分です。物理計算に、空間自体に対する物体Oの運動を考慮する必要は全くありません。
１８.高速移動により変化するのは私の主観的な時間と空間である
ところで、私が感じている時間と空間は、私の心が作り出したものです。決して外界にある時間と空間を直接感じている訳ではありません。しかし、私の内界にある「主観的時空間」は、外界の「客観的時空間」と一致する様に作られています。もしそうでなければ、私達が感じている主観的な時間空間に従って行動し外界に働きかけた時、その行為は失敗するからです。
そして私が高速で移動すると、「客観的時空間」と「主観的時空間」が相違します。つまり高速移動により、我々の「主観的時間」と「主観的空間」は下記のとおり「ローレンツ逆変換」します。
⑤x'=x√(1-v2/c2)+vt
⑥y'=y
⑦z'=z
⑨t'=t√(1-v2/c2)+vx/c2
高速移動すると、私の肉体を構成する粒子が動き難くなり、私はゆっくり動き・ゆっくり思考し・ゆっくり年を取ります。また、私の肉体は進行方向へ「ローレンツ収縮」します。この｢理｣により、私の主観的時空間は変化します。
そして、変化する内界の時間を「固有時」と言います。
しかし、外界の客観的な時間と空間は変化しません。変化しない外界の客観的な時間と空間を「絶対時間」「絶対空間」と言います。
もし、絶対時空間自体が変化してしまったら、もう変化していない時空間はどこにもありません。そうなると、外界の時空間が変化したと定義する基準となるものは、もう何処にもありません。つまり、時空間は一体「何に対して歪んでいるのか」説明が付きません。したがって、客観的時空間を変化させてはいけません。
１９.特殊相対性原理
この様に、v慣性系ではあらゆる力が√(1-v2/c2)倍に弱まり、物体の速度も静止時に比べて√(1-v2/c2)倍しか出ません。しかし、v慣性系の時計も√(1-v2/c2)倍ゆっくりと時を刻むので、vで移動する観測者Aは静止時と同じ速度vで物体Oは移動すると見えます。つまり、静止系に居てもv慣性系に居ても、物理現象は同じに見えます。
２０.CATBIRD完全変換
「ローレンツ変換」は片道でも「光速度不変」を仮設し、θ=0°(観測者Aと光が対面する形)又はθ=180°(観測者Aと光が並走する形)のケースでのみ、「ローレンツ変換」自体を使って逆変換し、元の値に戻すことが出来ました。
そこで私も遊び心で、片道でも「光速度不変」を仮設し、観測者Aと光の進む角度θにかかわらず、全ての角度で逆変換できる「万能変換式」を発明してみました。
それは、β=(vx/ct)とすると
①x'=(x-vt)/√(1-β2/c2)
②y'=y√{(c2-v2)/(c2-β2)}
③z'=z√{(c2-v2)/(c2-β2)}
④t'=(t-vx/c2)/√(1-β2/c2)
です。この①から④を「CATBIRD完全変換」と言います(2020/08/16am0:17)。
では、この「CATBIRD完全変換」で、光の進む座標を変換し、その変換された座標を今度は「CATBIRD完全変換」で逆変換して、元の座標に戻ることを確認します。
そして、変換後及び逆変換後の光の速度は、「光速度c」と不変であることを示します。
光の座標を(x,y,z)=(ct*cosθ,ct*sinθ,0)とします。半径ct[m]の内面鏡の中心Oから発した光は、鏡に反射してまたOに戻ります。静止時には
光の進んだ片道の距離L1=√(x2+y2+z2)=√{(ct*cosθ)2+(ct*sinθ)2+02}=ct[m]
光の進んだ時間t1=t[s]
です。
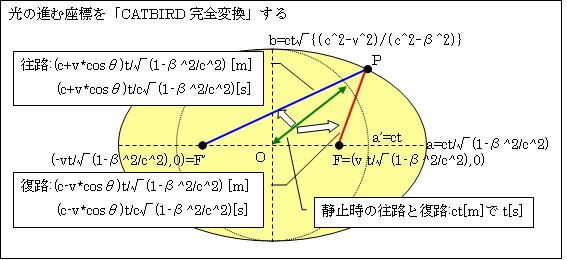次に、この内面鏡がv[m/s]で移動すると、「CATBIRD完全変換」されるので
光の進んだ片道の距離L2
=√(x'2+y'2+z'2)=√{(x-vt)/√(1-β2/c2)}2+[y√{(c2-v2)/(c2-β2)}]2+[z√{(c2-v2)/(c2-β2)}]2}
={√(1-v2/c2)/√(1-β2/c2)} √[{(x-vt)/√(1-v2/c2)}2+y2+z2]
= {√(1-v2/c2)/√(1-β2/c2)}√[{(ct* cosθ-vt)/√(1-v2/c2)} 2+(ct*sinθ)2+02]
= {√(1-v2/c2)/√(1-β2/c2)}t√{(c* cosθ-v)2*(c2/c2-v2)+c2 sin2θ}
= {√(1-v2/c2)/√(1-β2/c2)}t√{(c2cos2θ-2cv*cosθ+v2)*(c2/c2-v2)+(c2*sin2θ-v2 sin2θ) *(c2/c2-v2)}
={√(1-v2/c2)/√(1-β2/c2)} t√{(c2/c2-v2) (c2cos2θ-2cv*cosθ+v2+c2sin2θ-v2 sin2θ) }
={√(1-v2/c2)/√(1-β2/c2)}t√{(c2/c2-v2) (c2-2cv *cosθ+v2-v2(1- cos2θ) }
={√(1-v2/c2)/√(1-β2/c2)}t√{(c2/c2-v2) (c2-2cv *cosθ+v2-v2+v2cos2θ) }
={√(1-v2/c2)/√(1-β2/c2)}t√{(c2/c2-v2) (c2-2cv *cosθ+v2cos2θ) }
={√(1-v2/c2)/√(1-β2/c2)}t√{(c2/c2-v2) (c-v*cosθ) 2}
={√(1-v2/c2)/√(1-β2/c2)} (c-v*cosθ)t/√(1-v2/c2)
= (c-v*cosθ)t/√(1-β2/c2)[m]・・・(1)
です。L1=ctだったので
L2=(L1-vt* cosθ) /√(1-β2/c2)・・・(2)
です。
光の速度=c[m/s]なので
光の進んだ時間t2=(c-v*cosθ)t/√(1-β2/c2)[m]÷c[m/s]=(c-v*cosθ)t/c√(1-β2/c2)[s]=(L1-vt* cosθ) /c√(1-β2/c2)・・・(3)
です。
ct*cosθ=x、cosθ=x/ctなので
L2=(c-v*cosθ)t/√(1-β2/c2)= {c-(vx/ct)}t/√(1-β2/c2)= (t-vx/c2)c/√(1-β2/c2)[m]・・・(4)
t2={c-(vx/ct)}t/c√(1-β2/c2)=(t-vx/c2)/√(1-β2/c2)[s]・・・(5)
です。
これで
光の速度c'=(t-vx/c2)c/√(1-β2/c2)[m]÷(t-vx/c2)/√(1-β2/c2)[s]=c[m/s]
となり、光速度は不変です。
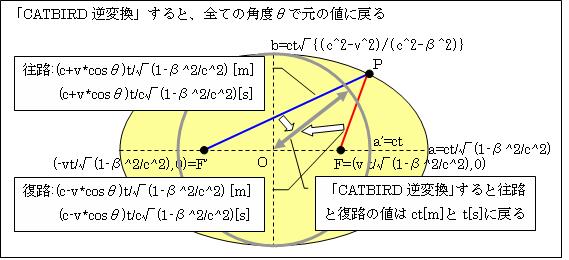このL2とt2の値を、①②③④の「CATBIRD完全変換」を使って逆変換すると、元のct[m]とt[s]に戻ります。そのためには、「CATBIRD完全変換」の(x,y,z,t)と(x',y',z',t')を入れ替え、vを-vにします。すると
⑤x=(x'+vt')/√(1-β2/c2)
⑥y=y'√{(c2-v2)/(c2-β2)}
⑦z=z'√{(c2-v2)/(c2-β2)}
⑧t=(t'+vx'/c2)/√(1-β2/c2)
です。即ち、(2)と(3)の(L1,t1)と(L2,t2)を入れ替え、vを-vにします。すると
L1=(L2+vt2* cosθ) /√(1-β2/c2) [m]・・・(6)
t1=(L2-vt2* cosθ) /c√(1-β2/c2) [s]・・・(7)
です。
この(6)(7)に(1)(3)を代入すると、β=(vx/ct)、ct*cosθ=x、cosθ=x/ct、β=v*cosθなので
L1=[{(c-v*cosθ)t/√(1-β2/c2)}+v* cosθ{(c-v*cosθ)t/c√(1-β2/c2)}]/√(1-β2/c2)
={(ct-vt*cosθ)/√(1-β2/c2)+v*cosθ(ct-vt*cosθ)/c√(1-β2/c2)}/√(1-β2/c2)
=(c2t-cvt*cosθ+cvt*cosθ-v2t*cos2θ)/c(1-β2/c2)
=(c2t-v2t*cos2θ)/{(c2-β2)/c}
=ct(c2-v2*cos2θ)/(c2-β2)
= ct(c2-v2*cos2θ)/(c2-v2*cos2θ)=ct[m]・・・(8)
と、元の値ct[m]に戻ります。
そして
t1=[{(c-v*cosθ)t/√(1-β2/c2)}+v* cosθ{(c-v*cosθ)t/c√(1-β2/c2)}]/c√(1-β2/c2)
={(ct-vt*cosθ)/√(1-β2/c2)+v*cosθ(ct-vt*cosθ)/c√(1-β2/c2)}/c√(1-β2/c2)
=(c2t-cvt*cosθ+cvt*cosθ-v2t*cos2θ)/c2(1-β2/c2)
=(c2t-v2t*cos2θ)/{(c2-β2)}
=t(c2-v2*cos2θ)/(c2-β2)= t(c2-v2*cos2θ)/(c2- v2*cos2θ)=t[s]・・・(8)
と、元の値t[s]に戻ります。
これで
光の速度c'=ct[m]÷t[s]=c[m/s]
となり、光速度は不変です。
(8)(9)のとおり、「CATBIRD完全変換」を使って逆変換すると、観測者Aと光との角度θにかかわらず、常に元の値に戻ります(^^)/。
２１.Kothimaro完全変換
更に「ローレンツ変換」に倣って、Y軸とZ軸を変化させない完全変換式を発明してみました。β=(vx/ct)とすると
①x'=√[(x-vt)2-{(β2t/v)-vt}2]/√(1-β2/c2)
②y'=y
③z'=z
④t'=(t-vx/c2)/√(1-β2/c2)
です。これを、「Kothimaro完全変換」と言います。(2020/08/23pm15:31)
「Kothimaro完全変換」の導き方を説明します。
L'=(c-v*cosθ)t/√(1-v2cos2θ/c2)
t'=(c-v*cosθ)t/c√(1-v2cos2θ/c2)
なら、この変換式を使って逆変換すれば、元の値に戻りました。したがって、この様になる「X軸Y軸Z軸の変換式」を求めれば良いのです。そして(x,y,z)=(ct*cosθ,ct*sinθ,0)とし
②y'=y
③z'=z
なので
L'=√(x'2+y'2+z'~2)=√{x'2+(ct*sinθ)2+02}
∴
x'2=L'2-c2t2sin2θ={(c-v*cosθ)t/√(1-v2cos2θ/c2)}2-c2t2sin2θ
=c2t2[{(c2-2cv*cosθ+v2cos2θ)/(c2-v2cos2θ)}-sin2θ]
=c2t2{(c2-2cv*cosθ+v2cos2θ-c2sin2θ+v2cos2θsin2θ)/(c2-v2cos2θ)}
=c2t2[{c2-2cv*cosθ+v2cos2θ-c2(1-cos2θ)+v2cos2θ(1-cos2θ)}/(c2-v2cos2θ)]
=c2t2{(c2-2cv*cosθ+v2cos2θ-c2+c2cos2θ+v2cos2θ-v2cos^4θ)/(c2-v2cos2θ)}
=c2t2{(-2cv*cosθ+2v2cos2θ+c2cos2θ-v2cos^4θ)/(c2-v2cos2θ)}
=c2t2{(c2cos2θ-2cv*cosθ+v2-v2-v2cos^4θ+2v2cos2θ-v2+v2)/(c2-v2cos2θ)}
=c2t2{(c*cosθ-v)2-(v*cos2θ-v)2}/(c2-v2cos2θ)}
=c2{(ct*cosθ-vt)2-(vt*cos2θ-vt)2}/(c2-v2cos2θ)}=⑤
⑥ct*cosθ=x、cosθ=x/ct、β=(vx/ct)、β=v*cosθ、β2=(v2x2/c2t2)なので
vt*cos2θ=vt(x2/c2t2)=vtx2/c2t2=β2×(t/v)=(β2t/v)=⑦
⑥と⑦を⑤に代入すると
⑤=c2[(x-vt)2-{(β2t/v)-vt}2}/(c2-v2cos2θ)]
=[(x-vt)2-{(β2t/v)-vt}2}]/(1-β2/c2)
∴
x'=√[(x-vt)2-{(β2t/v)-vt}2}]/√(1-β2/c2)=①
です。一方
t'=(c-v*cosθ)t/c√(1-v2cos2θ/c2)
=(t-vt*cosθ/c)/√(1-v2cos2θ/c2)
={t-vt*(x/ct)/c}/√(1-β2/c2)
=(t-vx/c2)/√(1-β2/c2)=④
です。
これで、「Kothimaro完全変換」が導かれました。「Kothimaro完全変換」で逆変換すると、全方位において、元の距離ct[m]・元の時間t[s]に戻ります(^^)/
▼思考の迷宮 目次
TopPage 思考の迷宮へ
according to CATBIRD
